Problema68: Estimación y Pruebas de Hipótesis

Ej68. Se sospecha que la calidad de los ladrillos procedentes de una fábrica R es peor que la que aseguran con un 12% de defectuosos. Por ello la constructora va a realizar un control de dichos ladrillos.

Se pide:

a) ¿Cuál es el tamaño de la muestra a analizar si deseamos determinar la proporción de ladrillos defectuosos de R con una precisión igual a 0.02, y nivel de confianza del 95%?.

b) De una muestra de 1000 se han detectado 140 en mal estado. ¿Con este resultado y por medio de un intervalo de confianza, podemos admitir como válida la proporción de defectuosos que asegura el fabricante R?.


Realizamos un recopilatorio de los datos ofrecidos en el enunciado del apartado:

· X ≡ 'Proporción de ladrillos en mal estado de la fábrica R'.
· P(X) = 0.12.

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema


Apartado a)

En este apartado nos dan los datos de la proporción de ladrillos defectuosos procedentes de la fábrica R y el error máximo que podemos cometer para obtener el tamaño de la muestra necesaria que cumpla con estos requisitos.

El error para un intervalo de confianza de proporción es el siguiente:

Siendo:

· E = 0.02
· p = 0.12
· q = 1 - 0.12 = 0.88

Obtenemos el parámetro α: 100(1 - α) = 95, despejamos: α = 0.05

· z_0.05/2 = z_0.025

Teniendo en cuenta las condiciones de la tabla de la Normal que se exponen en este blog:

0.5 - 0.025 = 0.475

Buscamos en la tabla de la Normal y obtenemos el valor: z = 1.96.

Pues ya estamos en disposición de obtener el tamaño de muestra mínimo que cumpla con las especificaciones dadas, simplemente, despejamos el parámetro n y sustituimos valores:

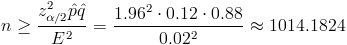
Por lo tanto, el tamaño mínimo muestral que se debe seleccionar para cumplir con los requisitos dados es de 1015 ladrillos.


Apartado b)

Nos piden realizar un intervalo de confianza de proporción, debemos verificar las siguientes condiciones:

· n = 1000 ≥ 30 OK.
· n·p = 1000·0.14 = 140 ≥ 5 OK.
· n·q = 1000·(1-0.14) = 880 ≥ 5 OK.

Por lo tanto, el intervalo de confianza a obtener es el siguiente:

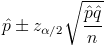
Ya disponemos de todos los datos necesarios para realizar un intervalo de confianza para la proporción de familias con coche al 95%, simplemente, sustituimos valores:

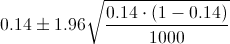
El intervalo de confianza es:

[0.118494, 0.161506]

Podemos comprobar fácilmente que la proporción de ladrillos defectuosos que dicen que vienen de la fábrica R (0.12) está dentro del intervalo que hemos obtenido, por lo tanto, podemos dar como válida la proporción de ladrillos defectuosos que vienen de la fábrica R.