Ej18. Se analiza una marca particular de margarina dietética para determinar el nivel de ácido graso poliinsaturado (en porcentaje). Se toma una muestra de seis paquetes y se obtienen los siguientes datos:
| 16.8. | 17.2. | 17.4. | 16.9. | 16.5. | 17.1. |
Determinar:
a) Prueba la hipótesis H0: μ = 17 contra H1: μ ≠ 17, utilizando para ello, α = 0.01. ¿Qué conclusiones podemos sacar?.
b) Calcula el p-valor de la prueba anterior.
En este problema, nos dan los datos de una muestra aleatoria, por lo que tenemos que obtener la media y la cuasi desviación estándar.
Para obtener la media:
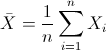
Por lo tanto:
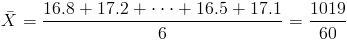
Para obtener la cuasi varianza:
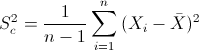
Por lo tanto:
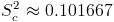
La prueba de hipótesis que plantea el enunciado del problema es:
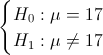
Es un contraste de media con desviación estándar desconocida, el estadístico es:
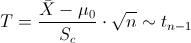
Apartado a)
Obtenemos el valor del estadístico:
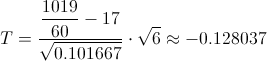
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:
T ≤ - tα/2, n -1, T ≥ tα/2, n -1
Para un nivel de significación de: α = 0.01, tenemos, en la tabla t-Student:
· tα/2, n -1 = t0.01/2, 6 -1 = t0.005, 5 = 4.0321
Comprobamos el valor del estadístico con la región crítica:
El valor del estadístico, -0.128037 está dentro del intervalo que compone la región crítica, (-4.0321, 4.0321), por lo tanto, aceptamos la hipótesis nula.
Esto quiere decir que, existen evidencias significativas de que la media, en porcentajes, del nivel de ácido graso poliinsaturado, para una marca particular de margarina dietética, es de 17.
Apartado b)
En este apartado, nos piden obtener el p-valor de la prueba del apartado anterior, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:
p-valor = 2 · P(T > |t|) = 2 · P(T > 0.128037) ≈ 2 · P(T > 0.1280)
Buscamos en las tablas de la t-Student con 5 grados de libertad, no encontramos el valor exacto, pero el valor más alto cercano al 0.1280 de las tablas corresponde a un área de cola de 0.4500, por lo tanto:
p-valor = 2 · P(T > 0.1280) = 2 · 0.4500 = 0.9
Hay que tener en cuenta que las tablas de la t-Student que dispone Aqueronte, albergan un área de cola desde 0.4500 hasta 0.0005, el valor para determinar el p-valor es, aproximadamente, 0.1280.
Si buscamos, con 5 grados de libertad, en las tablas t-Student, no encontramos un valor exacto ni inferior, sólo un nivel superior, que corresponde al área de cola: 0.4500.
Por lo tanto, el área de cola estará comprendido entre 0.4500 y 0.5000 (el área de cola para 0.5000 no está contemplado en las tablas), entonces, el p-valor estará comprendido entre los valores:
0.9 < p-valor < 1.0
Al ser el nivel de significación del problema, α = 0.01, menor que el p-valor, aceptamos la hipótesis nula.






5 comentarios:
hola buenas
lo primero decirte que tu trabajo es magnifico gracias por facilitar la vida de los estudiantes de estadistica.
y me gustaria si fuera posible que me dijeras como abordar los problemas del p-valor, ya que no los comprendo muy bien. gracias
Buenas:
El p-valor es una prueba más o herramienta tal como el intervalo de confianza o las pruebas de hipótesis.
Todas nos informan si nuestra suposición es cierta o no. Algunas de estas herramientas trabajan con datos elaborados (intervalos de confianza y pruebas de hipótesis) y otra, en este caso, el p-valor, trabaja con el nivel de significación (α).
El p-valor es una herramienta muy útil ya que nos dice el nivel de significación máximo en el que nuestra hipótesis será aceptada o rechazada.
Y para usar este tipo de herramienta, lo que debemos obtener es obtener aquel valor que supere el estadístico.
En este tema podrás encontrar multitud de ejemplos de cálculo del p-valor.
· PD: Por cierto, este ejercicio presenta una errata en el Apartado b), en el cálculo del p-valor, el estadístico es T no Z.
Ya está corregido.
Un saludo y gracias por tu comentario.
Buenas,gracias por el blog! ayuda muchisimo.
Mi duda es la parte de obtener el p-valor.Ni idea de porque habla de 5 grados de libertad,tampoco sé porque coge de la tabla el valor 0,4500.Vamos que no entiendo casi nada del apartado.Gracias y un saludo!
Buenas:
Vamos por partes:
· 1.- Para obtener el p-valor, necesitamos el valor del estadístico, en este problema concretamente, es el siguiente: T ≈ -0.128037.
· 2.- La región crítica está formada por dos valores (según nuestro formulario), por lo tanto, el p-valor se deberá obtener de la siguiente forma: p-valor = 2 · P(T > |t|)
· 3.- ¿Qué son los grados de libertad? Pues si te fijas en la expresión de la t-student, verás que su nomenclatura es algo tal que así: t_{α, v}
Donde:
* α: Nivel de significación.
* v: Grados de libertad.
En nuestro caso, es tal y como sigue: T ≤ - t_{α/2, n -1}, T ≥ t_{α/2, n -1}
Donde:
* n: Número de datos disponibles.
En nuestro problema, el número de datos disponibles son: 6 (los que están expuestos en el enunciado del problema)
¿De dónde sale entonces los 5 grados de libertad? Pues precisamente a la hora de sustituir datos: t_{α/2, n -1} = t_{0.01/2, 6 -1} = t_{0.005, 5} = 4.0321
Como puedes comprobar, los grados de libertad para este problema es: v = 5.
· 4.- ¿Por qué se escoge el valor 0.1280? Pues sencillamente porque es el valor del estadístico.
Y si hacemos una búsqueda inversa en la tabla t-student con 5 grados de libertad, veremos que no es posible hallarlo, pero el más cercano es 0.1322 y está a un área de cola de α = 0.4500.
Es por ello, que en este problema no podemos ofrecer un dato concreto para el p-valor pero, si podemos ofrecer en qué intervalo está, y en este caso es: 0.9 < p-valor < 1.0
Te recomiendo que te mires como trabajar el apartado que tenemos en el blog, de como trabajar con las tablas.
Un saludo.
Hola, me gustaría saber como resolver un ejercicio de probabilidad que es el siguiente:
Las 8 cavidades de una maquina de modelo por inyección producen conectores plásticos que caen en una banda de transporte común.Se toma una muestra de conectores, ¿cual es la probabilidad de que:
a) cinco muestras sucesivas hayan sido producidas en la cavidad uno del molde?
b)cinco muestras sucesivas hayan sido producidas en la misma cavidad del molde
c) cuatro de cinco muestras sucesivas hayan sido producidas en la cavidad uno del molde
Publicar un comentario