Problema17: Estimación y Pruebas de Hipótesis

Ej17. Un fabricante está interesado en el voltaje de salida de una fuente de alimentación utilizada en una computadora personal. Se supone que el voltaje de salida tiene una distribución normal, con desviación estándar 0.25 V.

El fabricante desea probar H0: μ = 5 V contra H1: μ ≠ 5 V, utilizando para ello, n = 8 unidades. Determinar:

a) Encuentre el valor de significación, α, para que la región de aceptación sea 4.85 ≤ X ≤ 5.15.

b) Si el fabricante desea la probabilidad del error tipo I para la prueba sea α = 0.05, ¿dónde debe localizarse la región de aceptación?


Realizamos una recopilación de los datos del problema:

· Tamaño de la muestra: n = 8.
· Desviación estándar: σ = 0.25.

La prueba de hipótesis que plantea el enunciado del problema es:

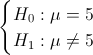
Al seguir una distribución normal y ser conocida la desviación estándar, el estadístico es:

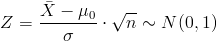
Apartado a)

En este apartado, debemos obtener el valor de significación para que se cumpla la región de aceptación dada, lo que tenemos que hacer es, tipificar a la normal:

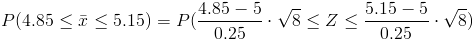
Aproximadamente es:

P(-1.697 ≤ Z ≤ 1.697)

Por lo tanto:

P(-1.697 ≤ Z ≤ 1.697) = (0.5 + Φ(1.697)) - [1 - (0.5 + Φ(1.697))] = 2·Φ(1.697)

Buscamos en la tabla de la Normal el valor 1.697, teniendo en cuenta que las tablas que dispone Aqueronte sólo dispone de dos cifras decimales, realizamos una interpolación lineal:

..1.69.....1.697......1.70
0.4545.....P..... .0.4554

De donde:

1.69 - 1.70.-> 0.4545 - 0.4554
1.69 - 1.697.-> 0.4545 - P

Calculamos:

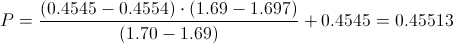
Por lo tanto:

P(-1.697 ≤ Z ≤ 1.697) = 2·Φ(1.697) = 2 · 0.45513 = 0.91026

Lo interesante para nosotros es el valor de Φ(1.697), ya que es el valor tipificado del nivel de significación, su valor es: Φ(1.697) = 0.45513.

Utilizamos cualquiera de las dos opciones de la región crítica para el caso de la prueba de hipótesis que estamos tratando:

Z ≤ - z_α/2 , Z ≥ z_α/2

Al fin y a cabo, nos interesa: _α/2, teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - α/2 = 0.45513

Despejamos el valor de significancia y obtenemos la solución a este apartado:

α = -(0.45513 - 0.5) · 2 = 0.08974

Apartado b)

Este apartado es la inversa del anterior, nos dan el nivel de significancia y debemos dar, la región de aceptación.

Para un nivel de significancia de 0.05 y teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - α/2 = 0.5 - 0.05/2= 0.4750

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.4750, y dicho valor, es 1.96.

Por lo tanto, la región de aceptación tipificada es:

P(-1.96 ≤ Z ≤ 1.96)

Operamos:

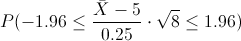
Despejamos X:

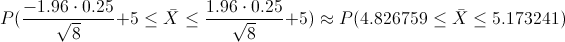
Por lo tanto, la región de aceptación es: 4.826759 ≤ X ≤ 5.173241.