Ej77. Se quiere elegir entre dos tipos de material textil para construir sistemas de amarre. Para ello se mide la tensión de rotura de varias cintas de prueba utilizando dos tipos de material.
Se toman 24 datos usando el material M1, obteniéndose x1 = 87 (kg/mm2 ) y s1 = 2. Se toman además 30 datos usando el material M2, obteniéndose x2 = 75 y s2 = 2.3.
Se sabe que las tensiones de rotura se distribuyen como una normal.Se supondrá, además, que las varianzas de ambas poblaciones son iguales.
Determinar:
a) Construir un intervalo de confianza del 95% de la diferencia de tensión de rotura media
b) Contrasta, con un nivel de significación del 1%, que el material M1 tiene mayor resistencia media que el M2.
· NOTA: x1 e x2 son las medias muestrales de los materiales M1 e M2 respectivamente.
Apartado a)
Nos piden obtener un intervalo de confianza para la diferencia de medias de ambos métodos con las varianzas son desconocidas de ambas muestras e iguales.
Para un 95%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.05.
Pasamos a confeccionar el intervalo de confianza para la diferencia de medias.
El siguiente paso es obtener los valores de:
Buscamos el valor en la tabla t-Student y no está disponible excatamente, por lo que realizamos una interpolación lineal:
..50..........52.......60
2.0086.....P.....2.0003
De donde:
50 - 60.-> 2.0086 - 2.0003
50 - 52..-> 2.0086 - P
Calculamos:
Necesitamos obtener el valor de Sp:
Sustituimos valores:
Ya disponemos todos los datos necesarios para obtener el intervalo bilateral de confianza al 95% de la diferencia de medias con varianzas desconocidas e iguales:
El intervalo de confianza bilateral al 95% es:
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:
Para un nivel de significación de: α = 0.01, tenemos, en la tabla t-Student:
Buscamos el valor en la tabla t-Student y no está disponible excatamente, por lo que realizamos una interpolación lineal:
..50..........52......60
2.4033.....P.....2.3901
De donde:
50 - 60.-> 2.4033 - 2.3901
50 - 52..-> 2.4033 - P
Calculamos:
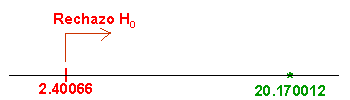
Realizamos una concepción gráfica de los datos hasta ahora obtenidos:
Esto quiere decir que, existen evidencias significativas de que la media de la tensión de rotura M1 es mayor que el del material M2.

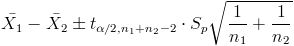
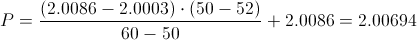
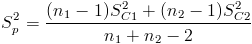
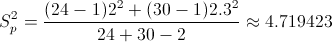
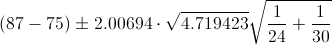
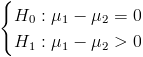
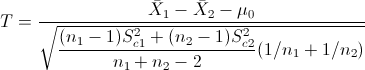
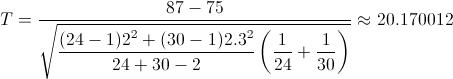
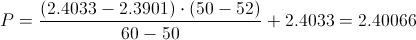




0 comentarios:
Publicar un comentario