Ej62. Una variable que se utiliza para comparar las características físicas de las nadadoras olímpicas con las de las corredoras es la circunferencia de la parte superior del brazo, en centímetros, mientras están relajadas.
Se dispone de los siguientes datos.
| Nadadoras | .. | Corredoras.. |
| n1 = 10 | n2 = 12 | |
| x1 = 27.3 cm | x2 = 23.5 cm | |
| S1 = 1.9 cm | S2 = 1.7 cm |
Supuesta normalidad, con α = 0.05, ¿hay razón suficiente para pretender que la media de la circunferencia de la parte superior del brazo sea mayor en las nadadoras que en las corredoras?
NOTA: Siendo x1 y x2 las medias de la circunferencia de la parte superior del brazo de las muestras dadas respectivamente.
Antes de abordar lo que nos piden en este problema, debemos saber si las varianzas de ambas muestras son iguales o no.
Prueba de hipótesis de igualdad de varianzas:
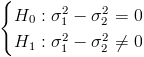
Es un contraste sobre igualdad de varianzas con medias desconocidas, el estadístico es:
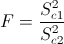
Obtenemos el valor del estadístico:
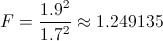
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:
F ≤ f1-α/2,n1-1,n2-1, F ≥ fα/2,n1-1,n2-1
Para un nivel de significación de: α = 0.05, tenemos en la tabla distribución F:
· f1-α/2,n1-1,n2-1 = f1-0.05/2, 10-1, 12-1 = f0.975,9,11 = 1/f1-0.975,11,9 = 1/f0.025,11,9
· fα/2,n1-1,n2-1 = f0.05/2, 10-1, 12-1 = f0.025,9,11Si buscamos en las tablas de la distribución F veremos que no se encuentra el valor exacto del primer elemento, para tal fin, aplicaremos interpolación lineal:
· Para el valor: f0.025,11,9
..10.....11....12
3.96....F.. .3.87
De donde:
10 - 12.--> 3.96 - 3.87
10 - 11.--> 3.96 - F
Calculamos:
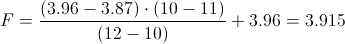
Por lo tanto, para un nivel de significación de: α = 0.05, tenemos:
· f1-α/2,n1-1,n2-1 = 1/f0.025,11,9 = 1/3.915 ≈ 0.255428
· fα/2,n1-1,n2-1 = f0.025,9,11 = 3.59Comprobamos el valor del estadístico con la región crítica:
El valor del estadístico, 1.249135 está dentro del intervalo que compone la región crítica, (0.255428, 3.59), por lo tanto, aceptamos la hipótesis nula.
Esto quiere decir que, existen evidencias significativas de que las varianzas de ambas muestras, son iguales.
En estos momentos, ya podemos obtener las conclusiones que nos requieren en el enunciado del problema.
Contraste sobre diferencias de medias con varianzas desconocidas e iguales:
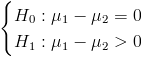
Es un contraste de diferencia de medias con desviación estándar desconocidas e iguales, el estadístico es:
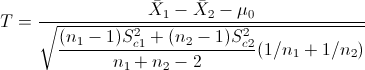
Obtenemos el valor del estadístico:
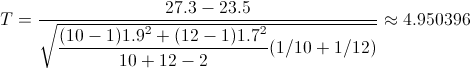
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:
T ≥ tα,n1+n2-2
Para un nivel de significación de: α = 0.05, tenemos, en la tabla t-Student:
· tα,n1+n2-2 = t0.05, 10+12-2 = t0.05, 20
Buscamos el valor en la tabla t-Student, y obtenemos el valor: 1.7247.
Realizamos una concepción gráfica de los datos hasta ahora obtenidos:
El valor del estadístico, 4.950396 se encuentra dentro de la región crítica, por lo tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa
Esto quiere decir que, existen evidencias significativas de que la media de la circunferencia de la parte superior del brazo de las nadadoras es mayor que el de las corredoras.







2 comentarios:
Ante todo, felicitarle por su blog,que espero que nos ayude a aprobar estádistica.
Sólo comentarle que cuando aplica F-snedecor para las varianzas, en la recta el intervalo correcto, ¿no sería (0.255428,3.59)y no (0.255428,3.915)?
Saludos
Rafa y Migue
Buenas:
Efectivamente, al realizar el dibujo explicativo del intervalo de confianza el intervalo superior estaba mal (puse el valor obtenido de la interpolación).
Aún así, no afecta a la resolución del ejercicio, es más, solo estaba ese dato mal en el dibujo ya que en el resto del problema, el intervalo estaba bien definido.
Un saludo y gracias por el apunte, ya está subsanado.
Publicar un comentario