Problema78: VAD

Ej78. El gerente local de una compañía de renta de automóviles compra neumáticos en lotes de 500 para aprovechar los descuentos por compras al mayor.

El gerente sabe, por experiencias anteriores, que el 1% de los neumáticos nuevos adquiridos en un determinado almacén salen defectuosos y se deben reemplazar durante la 1ra semana de uso.

Determinar la probabilidad de que en un envío de 500 neumáticos:

a) Haya solamente uno defectuoso.

b) No más de 3 defectuosos.

c) Ninguno defectuoso.

Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº de neumáticos defectuosos'.
· La variable aleatoria X sigue una distribución Binomial: X ~ B(500, 0.01).

Las características del tamaño de la muestra y la probabilidad relativamente baja que tiene, comprobaremos si podemos adaptar la distribución binomial a la de Poisson.

Para ello, debe cumplirse:

· n grande: n = 500 OK.

· n·p = 500·0.01 = 5 ≤ 7 OK.

Por lo tanto, se puede adaptar la variable aleatoria a la distribución de Poisson: X ~ P(5).

Pasamos a resolver los distintos apartados que nos ofrece el problema.

Apartado a)

Debemos obtener la siguiente probabilidad:

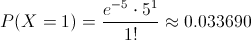
Por lo tanto, la probabilidad de que un neumático sea defectuoso de una muestra de 500 es de, aproximadamente 0.033690.

Apartado b)

La probabilidad que debemos obtener es la siguiente:

P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)

Al tener que calcularse el valor de varios elementos para obtener la solución a este apartado, vamos a emplear el software R para realizar dicha operación:

> ppois(3, 5)
[1] 0.2650259

Por lo tanto, la probabilidad de que como mucho, tres neumáticos sean defectuosos de una muestra de 500 es de, aproximadamente 0.265026.

Apartado c)

Debemos obtener la siguiente probabilidad:

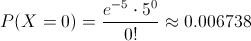
Por lo tanto, la probabilidad de que ningún neumático sea defectuoso de una muestra de 500 es de, aproximadamente 0.006738.