Problema57: Estimación y Pruebas de Hipótesis

Ej57. Puesto que un nivel de colesterol elevado es un factor de alto riesgo en el desarrollo de la aterosclerosis cardíaca y coronaria, es importante determinar los niveles a esperar en los diferentes grupos de edad.

Se realizó un estudio para comparar el nivel de colesterol en varones de entre 20 y 29 años frente a mujeres del mismo grupo de edad.

Se obtuvieron los siguientes resultados:

Varones	..	Mujeres..
n1 = 25		n2 = 31
x1 = 167.16		x2 = 178.12
S1 = 30		S2 = 32

Determinar, utilizando α = 0.05:

a) Comprobar si hay diferencias en las varianzas poblacionales.

b) ¿Existen diferencias significativas en los niveles medios de colesterol para hombres y mujeres?

NOTA: Siendo x₁ y x₂ las medias del nivel medio de nivel de colesterol en sangre de las muestras dadas respectivamente.


En este problema nos dan los datos muestrales necesarios para obtener los resultados que nos requieren.


Apartado a)

La prueba de hipótesis de igualdad de varianzas:

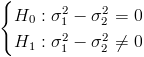
Es un contraste sobre igualdad de varianzas con medias desconocidas, el estadístico es:

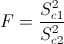
Obtenemos el valor del estadístico:

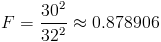
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

F ≤ f_{1-α/2,n1-1,n2-1}, F ≥ f_{α/2,n1-1,n2-1}

Para un nivel de significación de: α = 0.05, tenemos en la tabla distribución F:

· f_{1-α/2,n1-1,n2-1} = f_{1-0.05/2,25-1,31-1} = f_0.975,24,30 = 1/f_{1-0.975,30,24} = 1/2.21 ≈ 0.452489

· f_{α/2,n1-1,n2-1} = f_{0.05/2,25-1,31-1} = f_0.025,24,30 = 2.14

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 0.878906 está dentro del intervalo que compone la región crítica, (0.452489, 2.14), por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que las varianzas de ambas muestras, son iguales.

Apartado b)

Contraste sobre diferencias de medias con varianzas desconocidas e iguales:

Es un contraste de diferencia de medias con desviación estándar desconocidas e iguales, el estadístico es:

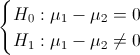
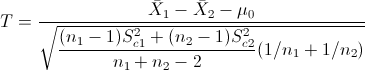
Obtenemos el valor del estadístico:

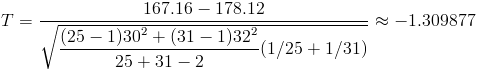
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

T ≤ - t_α/2,n1+n2-2, T ≥ t_α/2,n1+n2-2

Para un nivel de significación de: α = 0.05, tenemos, en la tabla t-Student:

· t_α/2,n1+n2-2 = t_{0.05/2,25+31-2}=t_0.025,54

Buscamos el valor en la tabla t-Student, y apreciamos que el número de grado de libertad 54 no está presente en las tablas, para hallarlo, realizamos una interpolación lineal:

..50...........54.........60
2.0086......T......2.0003

De donde:

50 - 60.-> 2.0086 - 2.0003
50 - 54.-> 2.0086 - T

Calculamos:

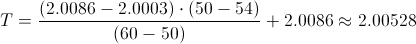
Realizamos una concepción gráfica de los datos hasta ahora obtenidos:

El valor del estadístico, -1.309877 se encuentra en el intervalo de la región crítica, (-2.00528, 2.00528), por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que no existen diferencias del nivel de colesterol entre hombres y mujeres.