Problema38: Estimación y Pruebas de Hipótesis

Ej38. Suponga que una muestra de 9 barras extraídas al azar de una producción arrojan una longitud media de 20 cm y que la longitud de las barras es una variable aleatoria normal con desviación típica de 3 cm.

Determinar:

a) ¿Cuál es el intervalo de confianza al 90% de nivel de confianza para estimar la longitud media de las barras?

b) ¿Cuántas barras adicionales deben ser medidas para aumentar la confianza del mismo intervalo al 95%?


Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:

· Media: X = 20.
· Desviación estándar: σ = 3.
· Tamaño de la muestra: n = 9.
· X ≡ 'Longitud de las barras'. Sigue una distribución Normal: X~N(20, 3).


Apartado a)

En este apartado nos piden realizar un intervalo de confianza para la media con varianza conocida y el tamaño de la muestra es menor que 30:

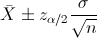
Para una confianza del 90%, obtenemos α:

100(1 - α) = 90

Despejamos el parámetro que nos interesa: α = 0.1. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.1/2 = z_0.05

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.05 = 0.45

Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:

..1.64.............Z..........1.65
0.4495........0.45.....0.4505

De donde:

1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z..-> 0.4495 - 0.45

Calculamos:

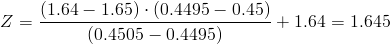
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 90%, simplemente, sustituimos valores:

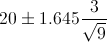
El intervalo de confianza bilateral al 90% es:

[18.355, 21.645]

Apartado b)

Este apartado es parecido al anterior, sólo que esta vez, debemos hallar el valor de la muestra dados los demás datos. El intervalo de confianza es el mismo, para la media con varianza conocida y el tamaño de la muestra menor que 30:

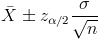
Para una confianza del 95%, obtenemos α:

100(1 - α) = 95

Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

El valor exacto se encuentra recogido en las tablas, z = 1.96.

Por lo tanto, ya disponemos de todos los datos necesarios para obtener el tamaño de la muestra con un intervalo de confianza de 95%, simplemente, sustituimos valores:

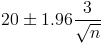
Para obtener el tamaño de la muestra, podemos escoger el intervalo inferior o el superior indistintamente, ya que ambos darán el mismo resultado, en este caso, utilizaremos el superior:

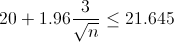
Despejamos el parámetro del tamaño de la muestra n, el valor es, aproximadamente:

n ≥ 12.776822

Como el tamaño de la muestra debe ser un número entero positivo, la solución a este apartado es que el tamaño de la muestra debe ser 13.