Ej40. Una máquina está programada para llenar recipientes con 10 litros de capacidad. Sin embargo, la variabilidad inherente a cualquier tipo de máquina es la causa de que las cantidades de contenido sean distintas de recipiente a recipiente.
Si la distribución del contenido que arroja la máquina en cada recipiente es normal con una desviación típica de 0.02 litros.
Determine la cantidad media del contenido para que sólo el 5% de los recipientes reciban menos de 10 litros.
Sea la variable aleatoria X, contenido que arroja la máquina en cada recipiente. El enunciado nos indica que se distribuye normalmente, por lo que usaremos la distribución normal para resolver el problema dado.
Cuya media es: μ y la desviación estándar: 0.02.
Por lo tanto, la variable continua aleatoria, sigue una distribución Normal: X ~ N(μ, 0.02)
En este problema, nos dan los datos de la probabilidad y debemos hallar el valor de la media que lo satisfaga.
Tenemos: P(X < . 10) = 0.05
Tipificamos:
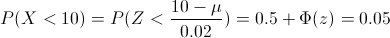
Despejamos:
Nos da un valor negativo, ésto indica que el valor de z se encuentra en la parte izquierda de la campana de Gauss. Las tablas que dispone Aqueronte, no ofrecen los valores negativos de la curva, pero no hay ningún problema, ya que la curva es simétrica, por lo que buscamos en la tabla el valor 0.45 que de un z válido.
Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:
..1.64.............Z..........1.65
0.4495........0.45.....0.4505
De donde:
1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z..-> 0.4495 - 0.45
Calculamos:
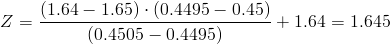
Por lo tanto, la cantidad media de producto, para los datos dados, será de:
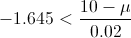
Despejamos μ y obtenemos la solución a este problema: μ < . 10.0329





2 comentarios:
en el probl 40 no hace correccion por continuidad y la hace en el probl 38 por que ?
Buenas:
No se aplica en este problema ninguna corrección de continuidad porque la variable de este problema es continua.
En cambio, la variable del problema 30, es una variable aleatoria discreta que sigue una distribución binomial pero que por sus circunstancias, se puede aproximar a una distribución normal.
Es por ello que al pasar una variable aleatoria discreta a una variable continua (cómo en este caso una distribución normal), hay que aplicar el factor de corrección.
Un saludo y gracias por tu comentario.
Publicar un comentario