Ej79. El pH del suelo es una variable importante cuando se diseñan estructuras que están en contacto con el terreno. Se tiene noticia de que el pH medio de un lugar destinado a la construcción es de 6.5.
Se tomaron nueve muestras del suelo del terreno y se obtuvieron los resultados siguientes de pH:7.3. 6.5. 6.4. 6.1. 6.0. 6.5. 6.2. 5.8. 6.7
Determinar:
a) Suponiendo la distribución del pH normal, ¿podemos mantener a un nivel de significación de 0.05 que el valor del pH medio del suelo tiene el valor afirmado más arriba?.
b) Sabiendo que la desviación típica del valor del pH es menor o igual que 0.5, ¿cuántos registros del pH serán necesarias para estimar el pH medio con un error de estimación menor o igual que 0.05 y un nivel de confianza del 99%?.
En este problema, nos dan los datos de una muestra aleatoria, por lo que tenemos que obtener la media y la cuasi desviación estándar.
Para obtener la media:
Por lo tanto:
Para obtener la cuasi varianza:
Por lo tanto:
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
La prueba de hipótesis que plantea el enunciado del problema es:
Es un contraste de media con desviación estándar desconocida, el estadístico es:
Obtenemos el valor del estadístico:
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:
Para un nivel de significación de: α = 0.05, tenemos, en la tabla t-Student:
Comprobamos el valor del estadístico con la región crítica:
Esto quiere decir que, existen evidencias significativas de que la media de pH del suelo es de 6.5.
Para refutar el estudio, vamos a obtener el p-valor de la prueba del apartado anterior, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:
Buscamos en las tablas de la t-Student con 8 grados de libertad, no encontramos el valor exacto, pero sí los valores dónde está comprendido.
Por lo tanto, el área de cola estará comprendido entre 0.2500 y 0.2000, entonces, el p-valor estará comprendido entre los valores:
Al ser el nivel de significación del problema, α = 0.05, menor que el p-valor, aceptamos la hipótesis nula.
Apartado b)
En este apartado nos piden obtener el números de muestras necesarias para estimar el pH medio dado unos datos iniciales: el error, la varianza y el nivel de confianza.
La expresión matemática de error para este tipo de variables es la siguiente:
Para una confianza del 99%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.01. El siguiente paso es obtener el valor de la z:
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.495, y dicho valor, no se encuentra de forma exacta, por lo que realizamos una interpolación lineal:
..2.57...........Z....... ..2.58
0.4949.....0.495.. .0.4951
De donde:
2.57 - 2.58.---> 0.4949 - 0.4951
2.57 - Z.---> 0.4949 - 0.495
Calculamos:
Sustituimos valores y despejamos el parámetro n:
Por lo tanto, el número de registros necesarios para estimar el pH medio con tales condiciones es de 664 muestras.

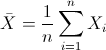
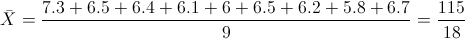
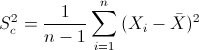
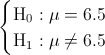
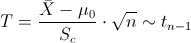
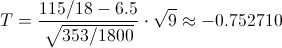

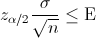
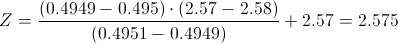
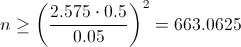




0 comentarios:
Publicar un comentario