Ej72. Se estudia la frecuencia con la que los alumnos de una Escuela Universitaria entran en la página web de la Escuela y se supone que cada alumno visita la web o no independientemente de lo que hacen sus compañeros.
Determinar:
a) Se supone que el tiempo (en días) que pasa entre dos visitas de un alumno sigue distribución exponencial de parámetro 4. Si ese alumno visitó hoy la página, ¿cuál es la probabilidad de que tarde 4 días o más en volver a visitarla?
b) Se sabe que el 25% no han entrado nunca la web, ¿cuál es la probabilidad de que haya más de 30 alumnos de entre 100 encuestados que no hayan entrado en la web?.
Apartado a)
Recopilamos los datos que nos ofrece el enunciado de este apartado:
· A ≡ 'Tiempo que pasa entre dos visitas de un alumno en días'.
· Dicho suceso sigue una distribución exponencial, A ~ Exp(4).
Debemos emplear la función de distribución acumulada de la distribución exponencial:
La probabilidad que debemos obtener es la siguiente:
Apartado b)
Realizamos una recopilación de datos que nos ofrece el apartado:
· Sea la variable aleatoria B, número de alumnos que no entran en la web.
· Tamaño de la muestra: N = 100 alumnos.
· La variable aleatoria discreta B sigue una distribución binomial: X ~ B(100, 0.25)
Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir las siguientes condiciones:
1. n·p ≥ 5 → 100·0.25 = 25 ≥ 5 OK.
2. n·q ≥ 5 → 100·(1-0.25) = 75 ≥ 5 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
Por lo tanto: B ~ N(n·p, √(n·p·q)) = N(25, √18.75).
Debemos obtener la siguiente probabilidad:
Aplicamos el factor de corrección:
Buscando en la tabla de la Normal, obtenemos la solución a este apartado:
Por lo tanto, la probabilidad de que haya más de treinta alumnos de entre 100, que no hayan entrado en la web es de, aproximadamente 0.102.

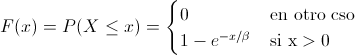
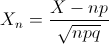
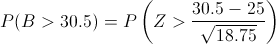




0 comentarios:
Publicar un comentario