Ej86. Se estudia la frecuencia con la que los alumnos de una Escuela Universitaria entran en la página web de la Escuela y se supone que cada alumno visita la web o no independientemente de lo que hacen sus compañeros.
Se sabe que el 25% no han entrado nunca la web, hallar :
a) ¿Cuál es la probabilidad de que haya que preguntar a 5 alumnos hasta encontrar 2 que no hayan entrado en la web?
b) ¿Cuál es la probabilidad de que ese alumno no visite la web 2 veces en una semana (7 días)?.
Sea la variable aleatoria discreta X, frecuencia que los alumnos de la escuela entran en la página web.
La probabilidad de que no entren en la web es de 0.25.
Con estos datos, pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
En este apartado, la variable aleatoria sigue una distribución Binomial Negativa con parámetros:
· Número de alumnos a encontrar que no hayan entrado en la web ≡ r = 2.
· Número de alumnos totales ≡ n = 5.
Necesitamos resolver:
Apartado b)
En este apartado, la variable aleatoria sigue una distribución de Poisson, de parámetro:
· n·p = 7·0.25 = 1.75
Sigue dicha distribución ya que el dato de una semana (siete días) es el que emplearemos cómo parámetro medio, por lo tanto: X~P(1.75).
Por lo tanto, la probabilidad a obtener es:
Por lo tanto, la probabilidad de que un alumno no visite la web dos veces en una semana es de, aproximadamente 0.266091.

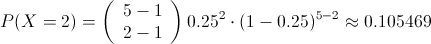
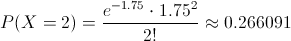




0 comentarios:
Publicar un comentario