Problema70: Estimación y Pruebas de Hipótesis

Ej70. Se consideran válvulas eléctricas del mismo tipo, procedentes de dos fábricas distintas. La duración de las válvulas es una variable aleatoria normal de parámetros μ y σ.

Para la primera fábrica, dicha distribución es N (μ₁ , 24), y para la segunda, N (μ₂ , 28).

Se extraen en las dos fábricas muestras aleatorias simples de tamaños respectivos n₁ = 10 y n₂ = 200. La duración media de las válvulas de la primera muestra es x₁ = 1452 h., mientras que en la segunda se obtiene x₂ = 1447 h.

¿Puede admitirse con un nivel de confianza del 95% que las dos fábricas producen válvulas con la misma duración media?.


Realizamos una recopilación de los datos del problema:

· X₁ ≡ 'Fábrica 1'. Sigue una distribución Normal: X₁ ~ N(μ₁, 24), n₁ = 10, x₁ = 1452.
· X₂ ≡ 'Fábrica 2'. Sigue una distribución Normal: X₂ ~ N(μ₂, 28), n₂ = 200, x₂ = 1447.

La prueba de hipótesis que plantea el enunciado del problema es:

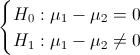
Es un contraste de diferencia de medias con desviación estándar conocida, el estadístico es:

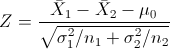
Obtenemos el valor del estadístico:

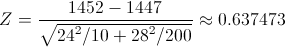
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≤ - z_α/2, Z ≥ z_α/2

Para un nivel de significación de: α = 0.05, tenemos, en la tabla Normal:

· z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

Tenemos que buscar el valor de z que satisfaga la probabilidad de 0.475, y dicho valor es: Z = 1.96.

Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, 0.637473 está dentro del intervalo que compone la región crítica, (-1.96, 1.96), por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir que, existen evidencias significativas de que la diferencia de medias son iguales, por lo tanto, ambas fábricas producen válvulas con la misma duración media.


Para corroborar la afirmación anterior, vamos a obtener el p-valor de la prueba, para dicho cálculo, debemos tener claro en que condiciones estamos, en nuestro caso, existen dos regiones críticas, por lo tanto, tenemos dos colas de probabilidad, el p-valor en estas condiciones, se calcula cómo:

p-valor = 2 · P(Z > |z|) = 2 · P(Z > 0.637473) = 2·[1 - P(Z ≤ 0.637473)] ≈ 2·[1 - (0.5 + Φ(0.64))] = 2·[0.5 - Φ(0.64)]

Buscamos en las tablas de la Normal el valor 0.64, el cual es 0.2389.

Sustituimos y obtenemos el p-valor:

p-valor = 2·[0.5 - Φ(0.64)] = 2·[0.5 - 0.2389] = 0.5222

Como el p-valor es mayor que el nivel de significación, aceptamos la hipótesis nula.