Problema21: Fiabilidad

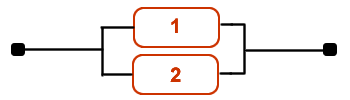
Ej21. Se tiene un sistema formado por 2 componentes en paralelo como el de la figura:

Donde los dos componentes tienen características similares. La avería de un componente es independiente del estado del otro componente. El sistema funciona si entre 1 y 2 es posible encontrar un camino de componentes que funcionen.

Determinar:

a) Supongamos que la duración de un componente (tiempo transcurrido desde que se conecta hasta que se avería) se puede modelizar con una exponencial y que la duración media de un componente es de 5000 horas. Calcula la probabilidad de que el sistema formado por ambos componentes en paralelo esté más de 10000 horas funcionando interrumpidamente.

b) Supongamos ahora que el sistema lleva ya 8000 horas funcionando sin averiarse. ¿Cuál será ahora la probabilidad de que llegue a las 10000 horas sin averiarse (es decir, que funcione al menos 2000 horas más)?.

Recopilamos información útil que nos ofrece el enunciado del problema:

· Ambos componentes siguen una distribución exponencial.
· MTTF = 5000.

Operamos en la función de la vida media:

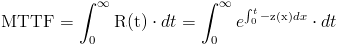
Una de las propiedades de la distribución exponencial es que la tasa de fallos es constante, por lo tanto:

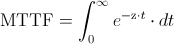
Realizamos el cambio de variable:

· x = -z·t
· dx = -z·dt

Y seguimos operando:

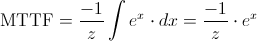
Deshacemos el cambio de variable:

· x = -z·t

Y, finalmente obtenemos:

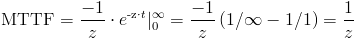
Por lo tanto, la tasa de fallos es:

Z(t) = 1/MTTF = 1/5000 = 0.0002

Hay que recordar que, la tasa de fallos para la distribución exponencial es constante para cualquier instante de t. Y la función de fiabilidad para ambos componentes es:

R(t) = e^-0.0002·t

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

El sistema que ahora nos ofrece este apartado es el siguiente:

Los elementos 1 y 2 están en paralelo:

· R_I(t) = 1 - (1 - R₁)·(1 - R₂) = 1 - (1 - e^-0.0002t)².

Ya estamos en condiciones de obtener la probabilidad que nos piden en este apartado:

P(X > 10000) = R_I(10000) = 1 - (1 - e^{-0.0002·10000})² ≈ 0.252355

Por lo tanto, la probabilidad de que el sistema dado esté funcionando más de 10000 horas interrumpidamente es de, aproximadamente 0.252355.


Apartado b)

En este apartado, nos piden obtener la probabilidad:

P(T > 8000 + 4000 | T > 8000)

Hay que tener en cuenta la propiedad de carencia de memoria de la distribución exponencial:

P(T > 8000 + 4000 | T > 8000) = P(T > 4000)

La solución a este apartado es:

P(T > 4000) = R_I(4000)= 1 - (1 - e^{-0.0002·4000})² ≈ 0.696761

Por lo tanto, la probabilidad de que el sistema llegue a las 10000 horas funcionando sin averiarse llevando ya 8000 horas, es de, aproximadamente 0.696761.