Ej71. El ayuntamiento de Jerez de la Frontera está considerando la posibilidad de levantar un edificio llamado "Ciudad del Flamenco". Una muestra aleatoria de 610 contribuyentes jerezanos revela que el 50.7% de los encuestados está en contra de dicho edificio.
Hallar un intervalo de confianza del 99% para la proporción de la población que desaprueba el levantamiento del edificio.
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del apartado:
· X ≡ 'Proporción de personas que estén en contra de la Ciudad del Flamenco'.
· P(X) = 0.507.
Nos piden realizar un intervalo de confianza de proporción, debemos verificar las siguientes condiciones:
· n = 610 ≥ 30 OK.
· n·p = 610·0.507 = 309.27 ≥ 5 OK.
· n·q = 610·(1-0.507) = 300.73 ≥ 5 OK.
Obtenemos el parámetro α: 100(1 - α) = 99, despejamos: α = 0.01
· z0.01/2 = z0.005
Teniendo en cuenta las condiciones de la tabla de la Normal que se exponen en este blog:
Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:
..2.57.............Z..........2.58
0.4949........0.495.....0.4951
De donde:
2.57 - 2.58.-> 0.4949 - 0.4951
2.57 - Z..-> 0.4949 - 0.495
Calculamos:
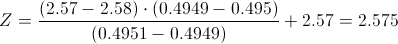
Por lo tanto, el intervalo de confianza a obtener es el siguiente:
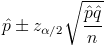
Ya disponemos de todos los datos necesarios para realizar un intervalo de confianza para la proporción de personas que rechazan la Ciudad del Flamenco al 99%, simplemente, sustituimos valores:
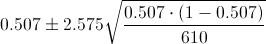
El intervalo de confianza es:





0 comentarios:
Publicar un comentario