Problema56: Estimación y Pruebas de Hipótesis

Ej56. En el análisis de un pigmento contenido en una cierta flor de una planta vegetal se obtuvieron los siguientes resultados experimentales, expresados como mg de pigmento por gramo de flor:

2.08.

2.11.

2.39.

2.08.

2.12.

2.23.

2.17.

2.11..

Considerando normalidad, calcular, a un nivel del 99%:

a) Un intervalo de confianza para el parámetro µ.

b) Un intervalo de confianza para el parámetro σ².


En este problema, nos dan los datos de una muestra aleatoria, obtendremos la información que nos será necesaria para la resolución de este problema.

El tamaño de la muestra es:

· n = 8

Para obtener la media:

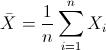
Por lo tanto:

·

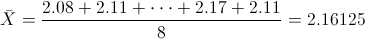
Para obtener la cuasi varianza:

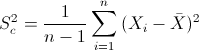
Por lo tanto, la cuasi desviación típica:

· S_c ≈ 0.105077

Para una confianza del 99%, obtenemos α:

100(1 - α) = 99

Despejamos el parámetro que nos interesa: α = 0.01.

Pasamos a resolver los distintos apartados que nos ofrece el problema.


Apartado a)

En este problema nos pide realizar un intervalo de confianza para la media con varianza desconocida y el tamaño de la muestra es menor que 30:

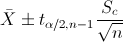
El siguiente paso es obtener el valor de la t-Student:

· t_α/2,n-1 = t_{0.01/2, 8-1} = t_{0.005, 7}

Buscamos el valor en la tabla t-Student, y obtenemos: 3.4995.

Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 99%, simplemente, sustituimos valores:

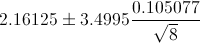
El intervalo de confianza bilateral al 99% es, aproximadamente:

[2.031242, 2.291258]

Apartado b)

En este apartado nos pide realizar un intervalo de confianza para la varianza con la media desconocida:

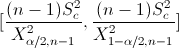
Para un nivel de significancia de: α = 0.01. El siguiente paso es obtener los valores de:

· X²_α/2,n-1 = X²_{0.01/2, 8-1} = X²_{0.005, 7}

· X²_1-α/2,n-1 = X²_{1-0.01/2, 8-1} = X²_{0.995, 7}

Buscamos el valor en la tabla ji-cuadrada, y obtenemos: 20.28 y 0.99 respectivamente.

Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la varianza con media desconocida, simplemente, sustituimos valores:

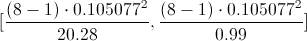
El intervalo de confianza bilateral al 99% es, aproximadamente:

[0.003811, 0.078069]