Ej67. El promedio de personas que llegan a la ventanilla de un banco por minuto durante las horas hábiles es una. Halle la probabilidad de que en un minuto dado:
a) No aparezcan clientes.
b) Hayan 3 o más clientes.
c) Hayan 3 o menos clientes.
Realizamos una recopilación de datos del enunciado del problema:
· X ≡ 'Nº de personas que llegan a la ventanilla de un banco'.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(1) persona/minuto.
Apartado a)
La probabilidad que debemos obtener es la siguiente:
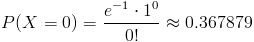
Por lo tanto, la probabilidad de que no aparezcan clientes es de, aproximadamente, 0.367879.
Apartado b)
La probabilidad que debemos obtener es la siguiente:
> 1-sum(dpois(c(0, 1, 2), 1))
[1] 0.0803014
Por lo tanto, la probabilidad de que aparezcan tres o más clientes es de, aproximadamente, 0.080301.
Apartado c)
La probabilidad que debemos obtener es la siguiente:
> ppois(3,1)
[1] 0.9810118
Por lo tanto, la probabilidad de que aparezcan tres o menos clientes es de, aproximadamente, 0.981012.





1 comentarios:
mil graacias me saco de un apuro
Publicar un comentario