Problema39: Estimación y Pruebas de Hipótesis

Ej39. En cierto proceso industrial se considera la variable aleatoria X ≡ 'Coste unitario de producción'. Se sabe que X tiene una distribución normal de media μ ydesviación típica 20.

Se toma una muestra aleatoria de 25 observaciones obteniéndose una media muestral de X = 120.

A partir de esta información muestral, calcule un intervalo de confianza del 95% para el coste unitario medio de producción.


Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:

· Media Muestral: X = 120.
· Desviación estándar: σ = 20.
· Tamaño de la muestra: n = 25.
· X ≡ 'Coste unitario de producción'. Sigue una distribución Normal: X~N(μ, 20).

Nos piden realizar un intervalo de confianza para la media con varianza conocida y el tamaño de la muestra es menor que 30:

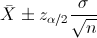
Para una confianza del 95%, obtenemos α:

100(1 - α) = 95

Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.05/2 = z_0.025

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.025 = 0.475

El valor exacto es z = 1.96.

Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 95%, simplemente, sustituimos valores:

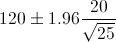
El intervalo de confianza bilateral al 95% es:

[112.16, 127.84]