Problema1: Fiabilidad

Ej1. Consideremos un sistema consistente en tres unidades conectadas en serie, cuyos tiempos de fallo tienen una distribución exponencial.

Las respectivas tasas de fallos, expresadas como número de fallos por hora, son:

· λ₁ = 0.0002

· λ₂ = 0.0005

· λ₃ = 0.0001

Calcular:

a) Obtén la función de fiabilidad del sistema.

b) ¿Cuál es la fiabilidad del sistema después de 150 horas de operación?

c) Halla la función de densidad de probabilidad del tiempo de fallo.

d) Calcula la tasa de fallo del sistema.

e) ¿Cuál es el tiempo medio de fallo del sistema?

f) ¿Cuál debe ser el período de garantía para una fiabilidad del 90%?

Recopilamos información útil que nos ofrece el enunciado del problema:

· Sistema en serie.
· Sigue una distribución exponencial.
· Tasa de fallos: λ₁ = 0.0002, λ₂ = 0.0005 y λ₃ = 0.0001

Teniendo en cuenta dicha información, la función de fiabilidad de cada unidad es:

· Unidad 1: R₁(t) = e^-0.0002·t

· Unidad 2: R₂(t) = e^-0.0005·t
· Unidad 3: R₃(t) = e^-0.0001·t

Ya disponemos de todos los datos necesarios para resolver los enunciados del problema.


Apartado a)

La función de fiabilidad del sistema en total, al ser en serie, es la multiplicación de la función de fiabilidad de cada unidad que lo compone:

R(t) = R₁(t) · R₂(t) · R₃(t) = e^-0.0002·t · e^-0.0005·t · e^-0.0001·t = e^{-(0.0002+0.0005+0.0001)·t}

Por lo tanto, la función de fiabilidad del sistema es:

R(t) = e^-0.0008·t

Apartado b)

Para este apartado, empleamos la función de fiabilidad obtenida en el anteriormente:

R(150) = e^-0.0008·t = e^-0.0008·150 ≈ 0.886920

Apartado c)

Por definición:

R(t) = 1 - F(t)

Despejamos la función acumulada:

F(t) = 1 - R(t)

Sabemos que la función de probabilidad es:

f(t) = F'(t) = [1 - R(t)]' = (-R(t))' = 0.0008·e^-0.0008·t

Apartado d)

Para obtener la tasa de fallos del sistema, empleamos su expresión matemática:

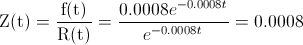
Al ser exponencial, la tasa de fallos es constante para cualquier valor de t.


Apartado e)

El tiempo medio hasta el fallo, MTTF, se obtiene mediante su expresión matemática tal y como se muestra a continuación:

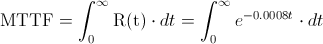
Realizamos el cambio de variable:

· x = -0.0008·t
· dx = -0.0008·dt

Sustituimos:

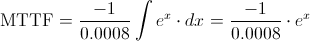
Deshacemos el cambio de variable:

· x = -0.0008·t

Por lo tanto:

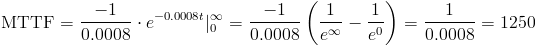
El tiempo medio hasta el fallo es de 1250 horas.


Apartado f)

En este apartado nos piden obtener el valor de t para una fiabilidad del 0.9:

R(t) = e^-0.0008·t = 0.9

Empleamos el logaritmo neperiano:

Ln(e^-0.0008·t)= Ln(0.9)

Operamos:

-0.0008·t= Ln(0.9)

Despejamos t para obtener la solución a este apartado:

t= Ln(0.9)/-0.0008 ≈ 131.700645 horas

Por lo tanto, para una fiabilidad del 90%, el período de garantía es de, aproximadamente, 131.700645 horas.