Fiabilidad

En este capítulo se abordará las expresiones matemáticas básicas para el estudio de la Fiabilidad.

Se abordará el estudio de los fallos que se producen aleatoriamente durante el funcionamiento de los sistemas y dispositivos, con objeto de prevenir consecuencias, establecer periodos de garantía y planear operaciones de mantenimiento.

Se entiende por fiabilidad de un componente, producto o dispositivo, a la probabilidad de que funcione correctamente, al menos, durante un tiempo especificado, en su aplicación prevista.

Se entiende por tiempo de fallo de un componente, producto o dispositivo, al tiempo que está funcionando hasta que se produce un fallo (T es una variable aleatoria que toma valores no negativos).


Función de Fiabilidad.

Se llama función de fiabilidad (o de supervivencia) de un componente, producto o dispositivo, a la función R: [0, ∞) pertenece a los números reales, definida como:

R(t) = P(T > t) = 1 - F(t)

Donde, F(t) es la función de distribución del tiempo de fallo.

Propiedades:

1. R(0) = 1 - F(0) = 1.
2. R(t) es una función decreciente.
3. Cuanto t → ∞, entonces, R(t) = 0


Esperanza de Tiempo de Fallo.

Denominado por las siglas: MTTF (mean time to failure), es expresada por:

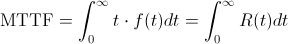
Donde f(t), es la función de densidad de probabilidad de T.


Tasa de Fallo.

Se llama tasa de fallo de un componente, producto o dispositivo, a la función R: [0, ∞) pertenece a los números reales, definida como:

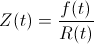
Donde f(t), es la función de densidad de probabilidad de T.

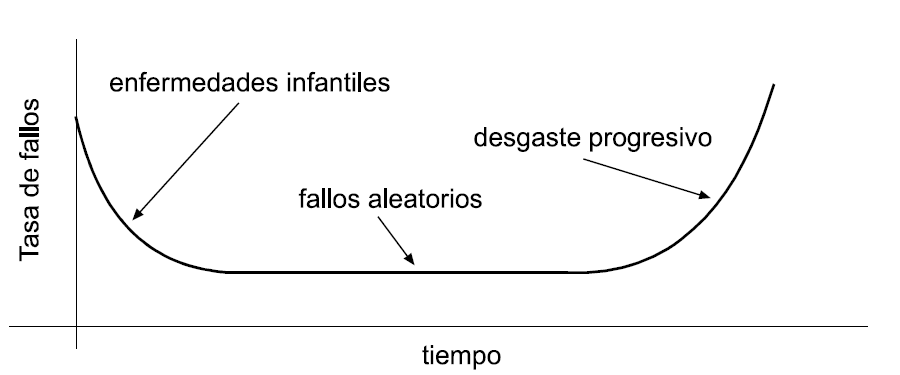
La representación gráfica de la tasa de fallo frente al tiempo es:

Distribución Exponencial.

· Función de Fiabilidad: R(t) = 1- F(t) = e^-k·t para t ≥ 0.

· Función de Densidad de Probabilidad: f(t) = k·e^-k·t para t ≥ 0.
· Tasa de Fallo: Z(t) = 1/β es constante para cualquier valor de t positivo.

Donde β = 1/k.


Distribución de Weibull.

Una variable aleatoria continua X, cuya función de densidad de probabilidad es de la forma:

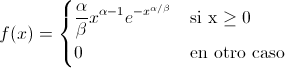
Se dice que tiene una distribución de Weibull de parámetros α y β. Se representa por: X ~ W(α, β).

Donde:

· α ≡ Parámetro de forma.
· β ≡ Parámetro de escala.

Tanto α como β deben ser positivos.

· Función de Fiabilidad: R(t) = 1- F(t) = e^-tα/β

· Tasa de Fallo: Z(t) = (α/β)·e^α-1

Distribución de Gompertz.

Una variable aleatoria continua X, cuya función de densidad de probabilidad es de la forma:

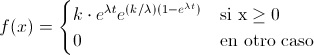
Se dice que tiene una distribución de Gompertz de parámetros k y λ. Se representa por: X ~ G(k, λ).

Tanto k como λ deben ser positivos.

· Función de Fiabilidad: R(t) = 1- F(t) = e^{(k/λ)·(1-eλ·t)}
· Tasa de Fallo: Z(t) = k·e^λ·t



Sistemas en Serie.

Es aquel cuyas unidades están conectadas entre sí de tal manera, que el fallo de una sóla de ellas implica el fallo del sistema completo.

Cada unidad de un sistema de este tipo se dice que está conectada en serie con las demás.

Un sistema en serie no es más fiable que la menos fiable de sus unidades.


Sistemas en Paralelo.

Es aquel cuyas unidades están conectadas entre sí de tal manera, que el sistema sólo falla si lo hacen todas sus unidades.

Cada unidad de un sistema de este tipo se dice que está conectada en paralelo con las demás.

Un sistema en paralelo es tan fiable como la más fiable de sus unidades.

---

A continuación, se disponen de una colección de problemas resueltos.

Problemas: Fiabilidad.
Problema 1	Problema 11	Problema 21
Problema 2	Problema 12	Problema 22
Problema 3	Problema 13	Problema 23
Problema 4	Problema 14
Problema 5	Problema 15
Problema 6	Problema 16
Problema 7	Problema 17
Problema 8	Problema 18
Problema 9	Problema 19
Problema 10	Problema 20