Problema16: Fiabilidad

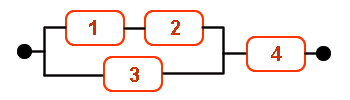
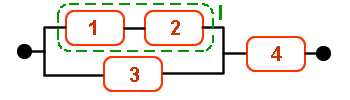
Ej16. Las cuatro unidades que forman el sistema de la figura son idénticas, independientes y tienen distribución de tiempo de fallo exponencial con MTTF = 1 (x1000 horas).

Determinar:

a) La fiabilidad en un instante cualquiera y la tasa de fallo en el instante inicial.

b) Si al cabo de 1000 horas la unidad 3 falla y no se repara ni sustituye, ¿en qué porcentaje habría disminuido la fiabilidad 1000 horas después con respecto al momento en que se produjo la avería?


Recopilamos información útil que nos ofrece el enunciado del problema:

· Sigue una distribución exponencial.
· MTTF = 1.

Operamos en la función de la vida media:

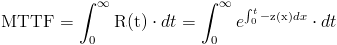
Una de las propiedades de la distribución exponencial es que la tasa de fallos es constante, por lo tanto:

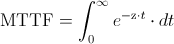
Realizamos el cambio de variable:

· x = -z·t
· dx = -z·dt

Y seguimos operando:

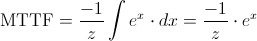
Deshacemos el cambio de variable:

· x = -z·t

Y, finalmente obtenemos:

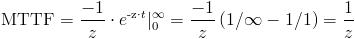
Por lo tanto, la tasa de fallos es:

Z(t) = 1/MTTF = 1/1 = 1

Hay que recordar que, la tasa de fallos para la distribución exponencial es constante para cualquier instante de t. Y la función de fiabilidad, para cada unidad del sistema, es:

R(t) = e^-t

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

Resolveremos este apartado, simplificando el circuito, dependiendo si los componentes están en serie o paralelo.

Los elementos 1 y 2 están en serie:

· R_I(t) = R₁ · R₂ = e^-t·e^-t = e^-2t

Los componentes I y 3 están en paralelo:

· R_II(t) = 1 - (1 - R_I)·(1 - R₃) = 1 - (1 - e^-2t)·(1 - e^-t) = 1 - (1 - e^-t - e^-2t + e^-3t) = e^-t + e^-2t - e^-3t

Los componentes II y 4 están en serie:

· R_III(t) = R_II·R₄ = (e^-t + e^-2t - e^-3t)·e^-t = e^-2t + e^-3t - e^-4t

Por lo tanto, la fiabilidad en un instante cualquiera t, viene determinada por la expresión:

R_III(t) = e^-2t + e^-3t - e^-4t

Al ser una distribución exponencial, la tasa de fallo es constante y por ende igual, en cualquier instante de tiempo t, por lo tanto, la tasa de fallo, calculada anteriormente, es:

Z(t) = 1/MTTF = 1/1 = 1

Aún así, vamos a demostrarlo, para ello, empleamos la expresión matemática de la tasa de fallos:

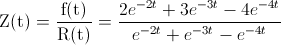
Siendo:

· f(t) = [F(t)]' = (1-R(t))' = -R(t)' = -(-2e^-2t -3e^-3t +4e^-4t) = 2e^-2t + 3e^-3t - 4e^-4t

En el instante inicial, t = 0:

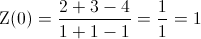
Queda demostrado nuestro razonamiento inicial.


Apartado b)

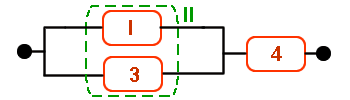
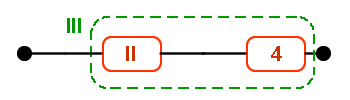
Si la unidad 3 falla, y no se repara ni se sustituye, tenemos el siguiente sistema:

Los componentes 1, 2 y 4 están en serie:

· R_I(t) = R₁·R_2·R₄ = (e^-t)³ = e^-3t

Para calcular la disminución de la fiabilidad, 1000 horas después, con respecto al momento en que se produjo la avería, empleamos la siguiente expresión:

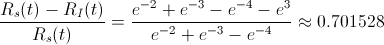
Siendo:

· R_s(t) ≡ La fiabilidad del sistema inicial, calculado en el apartado anterior, antes de fallar la unidad 3.
· R_I(t) ≡ La fiabilidad del sistema después de fallar la unidad 3.

En tantos por ciento, habrá disminuido, aproximadamente, un 70.15%.