Problema13: Fiabilidad

Ej13. El tiempo de fallo de un dispositivo tiene una distribución de probabilidad con función de densidad:

f(t) = t·e^-t

Para t ≥ 0, t en meses, determinar:

a) La fiabilidad.

b) Pasados dos meses funcionando, halla la probabilidad de que el dispositivo falle antes de 15 días (suponer, por sencillez, que todos los meses tienen 30 días).

c) ¿Tiene el dispositivo la propiedad de carencia de memoria?.


Apartado a)

En este apartado nos piden obtener la fiabilidad dada la función de densidad de probabilidad, para ello, emplearemos la relación de la función de densidad y la función de fiabilidad:

R(t) = 1 - F(t)

Integrando la función de probabilidad entre 0 y t, obtenemos la función de densidad acumulada:

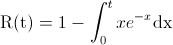
Realizamos la integral por partes:

· u = x...........: du = dx
· v = ʃe^-xdx..: v = -e^-x

Sustituimos:

R(t) = 1 - [-x·e^-x + ʃe^-xdx] = 1 + x·e^-x - ʃe^-xdx = 1 + x·e^-x + e^-x = 1 + e^-x·(x + 1)|^t₀ = 1 +[e^-t·(t + 1) - (0 + 1)] = e^-t·(t + 1)

Por lo tanto, la función de fiabilidad es, para t ≥ 0:

R(t) = e^-t·(t + 1)

Apartado b)

Hay que tener en cuenta que el tiempo de fallo está dado en meses, pero el enunciado nos pide la probabilidad de que falle antes de 15 días (dado que ya lleva dos meses funcionando).

Lo que tenemos que hacer, antes que nada, es pasar los 15 días a meses, con una simple regla de tres (considerando que los meses tienen 30 días):

30 --- 1
15 --- x

Por lo tanto: x = 0.5 meses (15 días).

Nos piden obtener la siguiente probabilidad:

Simplificamos:

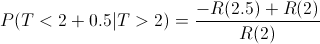
Y sustituimos valores:

Apartado c)

Para que se cumpla la propiedad de carencia de memoria, se debe cumplir:

P(T < .2 + 0.5|T > 2) = P(T < .0.5) = e^-0.5·(0.5 + 1) ≈ 0.090204

Se puede comprobar, que no dan el mismo resultado (respecto al apartado anterior), por lo tanto, no se cumple la propiedad de carencia de memoria (no es una distribución exponencial ni geométrica).