Ej12. El sistema de la figura está constituido por los componentes: A, B C D y E. Las probabilidades de cada uno de éstos que funcione más de 1000 horas son:
· pA = 0.9
· pB = 0.8
· pC = 0.85
· pD = 0.95
· pE = 0.8
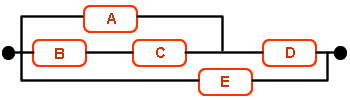
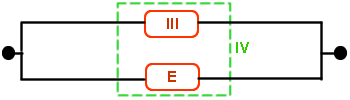
El sistema está configurado tal y como se muestra en la siguiente figura:
Si los componentes funcionan independientemente, halla la fiabilidad del sistema a las 1000 horas
Resolveremos este ejercicio simplificando el circuito, dependiendo si los componentes están en serie o paralelo.
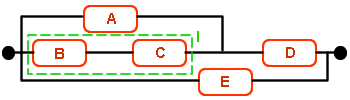
Los elementos B y C están en serie:
· RI(t) = RB · RC = 0.8·0.85 = 0.68
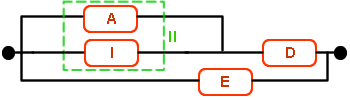
Los componentes I y A están en paralelo:
· RII(t) = 1 - (1 - RA)·(1 - RI) = 1 - (1 - 0.9)·(1 - 0.68) = 0.968
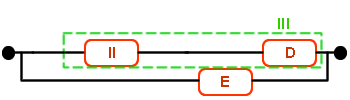
Los componentes II y D están en serie:
· RIII(t) = RII·RD = 0.968·0.95 = 0.9196
Y por fin, los elementos III y E están en paralelo, y obtenemos la solución a este problema:
· RIV(t) = 1 - (1 - RIII)·(1 - RE) = 1 - (1 - 0.9196)·(1 - 0.8) = 0.98392
Por lo tanto, la solución a este problema era calcular la fiabilidad del sistema a las 1000 horas, resulta ser: 0.98392, una fiabilidad alta.
· RI(t) = RB · RC = 0.8·0.85 = 0.68
Los componentes I y A están en paralelo:
· RII(t) = 1 - (1 - RA)·(1 - RI) = 1 - (1 - 0.9)·(1 - 0.68) = 0.968
Los componentes II y D están en serie:
· RIII(t) = RII·RD = 0.968·0.95 = 0.9196
Y por fin, los elementos III y E están en paralelo, y obtenemos la solución a este problema:
· RIV(t) = 1 - (1 - RIII)·(1 - RE) = 1 - (1 - 0.9196)·(1 - 0.8) = 0.98392
Por lo tanto, la solución a este problema era calcular la fiabilidad del sistema a las 1000 horas, resulta ser: 0.98392, una fiabilidad alta.





0 comentarios:
Publicar un comentario