Problema14: Fiabilidad

Ej14. Se conecta en serie un dispositivo que presenta una función de fiabilidad:

R(t) = e^-t·(t + 1)

Para t ≥ 0, t en meses, con otro dispositivo que tiene una tasa de fallo de 0.1. Determinar:

a) La fiabilidad del sistema a los tres meses.

b) La tasa de fallo del sistema a los tres meses.


Recopilamos información útil que nos ofrece el enunciado del problema:

· Primer Dispositivo: Función de fiabilidad es: R₁(t) = e^-t·(t + 1).
· Segundo Dispositivo: Tasa de fallos: Z(t) = 0.1, es constante, sigue una distribución exponencial.
· Ambos dispositivos están conectados en serie.

Por lo tanto, la función de fiabilidad del segundo dispositivo es:

R₂(t) = e^-0.1·t

Ya disponemos de los datos necesarios para resolver los respectivos apartados.


Apartado a)

En este apartado nos piden obtener la fiabilidad a los tres meses del sistema compuestos por ambos dispositivos conectados en serie.

Lo primero que haremos, es obtener la función de fiabilidad para cualquier instante de tiempo de fallo:

R(t) = R₁(t)·R₂(t) = e^-t·(t + 1)·e^-0.1·t = e^-(1+0.1)t·(t + 1) = e^-1.1t·(t + 1)

Por lo tanto, a los tres meses:

R(3) = e^-1.1·3·(3 + 1) ≈ 0.147533

Apartado b)

En este apartado nos piden obtener la tasa de fallos del sistema completo, para ello, necesitamos saber antes, la expresión de la función de probabilidad:

f(t) = F'(t) = [1 - R(t)]' = [-R(t)]' = -[e^-1.1t·(t + 1)]' = 1.1e^-1.1t·(t + 1) - e^-1.1t = e^-1.1t·[1.1·(t + 1) - 1]

Ahora, podemos calcular la tasa de fallos para cualquier instante de tiempo de fallo, por definición:

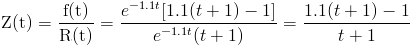
Por lo tanto, a los tres meses:

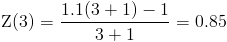
Podemos observar fácilmente que la tasa de fallo del sistema no es constante, sino que varía para distintos instantes de tiempo de fallo, t.