Problema2: Fiabilidad

Ej2. Se sabe que ciertos componentes tienen vida media 1000 horas y que su función de fiabilidad sigue el modelo exponencial.

Determinar:

a) La tasa de fallos.

b) La fiabilidad a las 10 y a las 1000 horas.

c) Si uno de estos componentes ha estado funcionando durante 1000 horas, ¿cuál es la probabilidad de que deje de hacerlo en las próximas 10 horas?.

Recopilamos información útil que nos ofrece el enunciado del problema:

· Sigue una distribución exponencial.
· MTTF = 1000.


Apartado a)

Operamos en la función de la vida media:

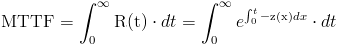
Una de las propiedades de la distribución exponencial es que la tasa de fallos es constante, por lo tanto:

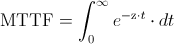
Realizamos el cambio de variable:

· x = -z·t
· dx = -z·dt

Y seguimos operando:

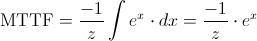
Deshacemos el cambio de variable:

· x = -z·t

Y, finalmente obtenemos:

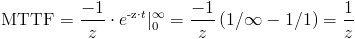
Por lo tanto, la tasa de fallos es:

Z(t) = 1/MTTF = 1/1000 = 0.001

Hay que recordar que, la tasa de fallos para la distribución exponencial es constante para cualquier instante de t. Y la función de fiabilidad es:

R(t) = e^-0.001·t

Apartado b)

Para este apartado, empleamos la función de fiabilidad:

· R(10) = e^-0.001·t = e^-0.001·10 ≈ 0.990050
· R(1000) = e^-0.001·t = e^-0.001·1000 ≈ 0.367879

Observamos que al aumentar el tiempo de fallo, la fiabilidad es menor.


Apartado c)

En este apartado, nos piden obtener la probabilidad:

P(T < . 1000 + 10 | T > 1000)

Hay que tener en cuenta la propiedad de carencia de memoria de la distribución exponencial:

P(T < . 1000 + 10 | T > 1000) = P(T < . 10)

Por lo tanto, la solución a este apartado es:

P(T < . 10) = 1 - R(10) = 1 - e^-0.001·10 = 1 - 0.990050 = 0.00995