Problema5: Fiabilidad

Ej5. Un aparato tiene una tasa de fallo constante con una duración de vida media de 500 horas. Determinar:

a) La probabilidad de que esté funcionando a las 100 horas.

b) Las horas que puede funcionar este aparato sin que la fiabilidad baje de 0.95.

Recopilamos información útil que nos ofrece el enunciado del problema:

· Tasa de fallo: Constante, por lo tanto, estamos ante una distribución exponencial.
· Esperanza del tiempo de fallo: MTTF = 500 horas.

Operamos en la función de la vida media:

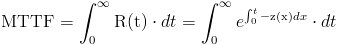
Una de las propiedades de la distribución exponencial es que la tasa de fallos es constante, por lo tanto:

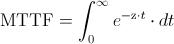
Realizamos el cambio de variable:

· x = -z·t
· dx = -z·dt

Y seguimos operando:

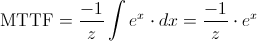
Deshacemos el cambio de variable:

· x = -z·t

Y, finalmente obtenemos:

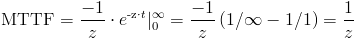
Por lo tanto, la tasa de fallos es:

Z(t) = 1/MTTF = 1/500 = 0.002

Hay que recordar que, la tasa de fallos para la distribución exponencial es constante para cualquier instante de t. Y la función de fiabilidad es:

R(t) = e^-0.002·t

Apartado a)

Empleamos la función de fiabilidad:

R(100) = e^-0.002·t = e^-0.002·100 ≈ 0.818731

Apartado b)

En este caso, debemos hallar t dada una fiabilidad:

R(t) = e^-0.002·t = 0.95

Empleamos logaritmo neperiano en ambas partes de la igualdad:

ln(e^-0.002·t ) = ln(0.95)

Seguimos operando:

-0.002·t = ln(0.95)

Despejamos t y obtenemos la solución a este apartado:

t = - ln(0.95)/0.002 ≈ 25.646647 horas

Por lo tanto, para una fiabilidad del 95%, son necesarias, como máximo, 25.646647 horas.