Problema4: Fiabilidad

Ej4. Un determinado producto tiene una tasa de fallos acumulada H(t) = e^0.05·t, t > 0 (t en años), determinar:

a) La función de densidad de probabilidad.

b) Calcula la probabilidad de que un producto de esta clase al azar, falle pasados 5 pero no después de 10 años.

Recopilamos información útil que nos ofrece el enunciado del problema:

· Tasa de fallos acumulada: H(t) = e^0.05·t.

La función de fiabilidad, dada la tasa de fallos acumulada, es:

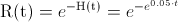
Apartado a)

En este apartado nos piden obtener la función de densidad de probabilidad:

f(t) = [1 - R(t)]' = [-R(t)]'

Realizando la derivada obtenemos la solución a este apartado:

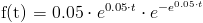
Apartado b)

Nos piden obtener la siguiente probabilidad:

P(5 < .T < .10) = [1 - R(10)] - [1 - R(5)] = -R(10) + R(5)

Sustituyendo valores en la función de fiabilidad obtenemos la solución a este apartado:

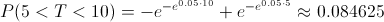
La fiabilidad es baja.