Problema6: Fiabilidad

Ej6. Un sistema está formado por tres componentes conectados en serie que funcionan independientemente. Suponiendo que el tiempo de fallo de los mismos, medido en horas, sigue una distribución exponencial de media 1000, 3000 y 6000 horas respectivamente, calcula la probabilidad de que el sistema no falle antes de 100 horas.


Recopilamos información útil que nos ofrece el enunciado del problema:

· Distribución exponencial: Tasa de fallo constante.
· Sistema en serie: La fiabilidad del sistema es el resultado del producto de la fiabilidad de cada elemento que lo compone.
· Media: MTTF₁ = 1000, MTTF₂ = 3000 y MTTF₃ = 6000

Operamos en la función de la vida media:

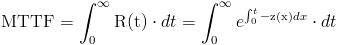
Una de las propiedades de la distribución exponencial es que la tasa de fallos es constante, por lo tanto:

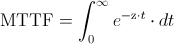
Realizamos el cambio de variable:

· x = -z·t
· dx = -z·dt

Y seguimos operando:

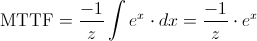
Deshacemos el cambio de variable:

· x = -z·t

Y, finalmente obtenemos:

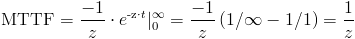
Por lo tanto, la tasa de fallo de cada componente es:

· Z₁(t) = 1/1000.
· Z₂(t) = 1/3000.
· Z₃(t) = 1/6000.

La fiabilidad del sistema en serie compuesto por tres elementos es el producto de cada uno de ellos:

R(t) = R₁(t) · R₂(t) · R₃(t) = e^-(1/1000)·t · e^-(1/3000)·t · e^-(1/6000)·t

Por lo tanto, la función de fiabilidad del sistema es:

R(t) = e^-0.0015·t

Que el sistema no falle antes de las 100 horas es: P(T > 100), operamos:

P(T > 100) = 1 - P(T ≤ 100) = 1 - F(100) = 1 - [1 - R(100)] = R(100)

Por lo tanto:

P(T > 100) = R(100) = e^-0.0015·100 ≈ 0.860708