Ej7. Un dispositivo tiene una tasa de fallos exponencial Z(t) = λ·eλ·t, t en horas, que en el instante inicial vale 0.002. Determinar:
a) La función de fiabilidad.
b) ¿Cuánto tiempo ha de pasar para que la fiabilidad se reduzca un 90%?
c) ¿Cuál es la probabilidad de que el dispositivo falle después de 100 horas pero antes de 500?
Recopilamos información útil que nos ofrece el enunciado del problema:
· Tasa de fallo: Z(t) = λ·eλ·t.
· Tasa de fallo en t = 0 (instante inicial): Z(0) = λ·eλ·0 = λ = 0.002
Apartado a)
Nos piden obtener la función de fiabilidad:
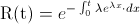
Realizamos el cambio de variable:
· m = λx
· dm = λdx
Y seguimos operando:
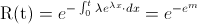
Deshacemos el cambio de variable:
· m = λx
Y, finalmente obtenemos:
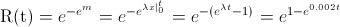
Apartado b)
Nos piden hallar el valor del tiempo de fallo para que la fiabilidad sea 90%:
P(T < . t) = F(t) = 1 - R(t) = 0.9
Por lo tanto:
R(t) = 1 - 0.9 = 0.1
Sustituyendo los valores, nos encontramos con la siguiente expresión:
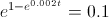
Empleamos el logaritmo neperiano para operar la igualdad:
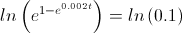
Operamos:
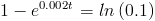
Despejamos la variable del tiempo de fallo t, para obtener la solución a este apartado:
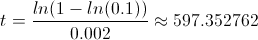
Esto quiere decir que, el tiempo que ha de pasar para que la fiabilidad se reduzca en un 90% es, aproximadamente, 597.352762 horas.
Apartado c)
Nos piden obtener la probabilidad siguiente:
P(100 < .T < .500) = [1 - R(500)] - [1 - R(100)] = -R(500) + R(100)
Sustituyendo por sus expresiones:
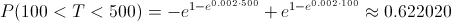





0 comentarios:
Publicar un comentario