Ej8. Durante las pruebas de fatiga de un colector de dinamo de automóvil, se ha demostrado que el número de kilómetros hasta el fallo sigue una distribución de Weibull de parámetros α = 3 y β = 180 0003 km, determinar:
a) La fiabilidad del aparato a los 15000 y a los 30000 km..
b) ¿Qué período de garantía, medido en número de kilómetros, se puede ofrecer al comprador de modo que la probabilidad de que un colector no falle durante el mismo sea al menos del 95%?
Recopilamos información útil que nos ofrece el enunciado del problema:
· Distribución de Weibull: W(3 , 180 0003).
La función de fiabilidad de la distribución de Weibull viene dada por la siguiente expresión:
R(t) = e-tα/β
En nuestro caso, sustituyendo valores:
R(t) = e-t3/1800003
Donde:
· α ≡ Parámetro de forma.
· β ≡ Parámetro de escala.
Apartado a)
Nos piden obtener la función de fiabilidad en dos instantes de tiempo de fallo:
· Para 15000 km ≡ R(15000) = e-150003/1800003 ≈ 0.999422.
· Para 30000 km ≡ R(30000) = e-300003/1800003 ≈ 0.995381.
Se puede observar que a más kilómetros, la fiabilidad baja.
Apartado b)
Nos piden hallar el valor del tiempo de fallo, en kilómetros, para que la fiabilidad sea 95%:
P(T > t) = 1 - P(T ≤ t) = 1 - F(t) = 1 - [1 - R(t)] = R(t) = 0.95
Sustituyendo los valores, nos encontramos con la siguiente expresión:
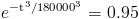
Empleamos el logaritmo neperiano para operar la igualdad:
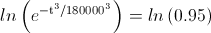
Operamos:
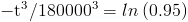
Despejamos la variable del tiempo de fallo t, para obtener la solución a este apartado:
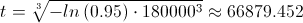
Esto quiere decir que, el periódo de garantía es de 66 879.452 km.
0 comentarios:
Publicar un comentario