Problema19: Fiabilidad

Ej19. Un sistema serie está formado por 10 unidades idénticas y siguen una distribución exponencial del tiempo de fallo con media β = 1000 horas.

En paralelo con este sistema se coloca otra unidad como las demás. ¿Cuáles son la fiabilidad y la tasa de fallos del sistema completo a las 50 horas?.


Recopilamos información útil que nos ofrece el enunciado del problema:

· Distribución exponencial: Tasa de fallo constante.
· Sistema en serie: La fiabilidad del sistema es el resultado del producto de la fiabilidad de cada elemento que lo compone.
· Media: MTTF = β = 1000.

Operamos en la función de la vida media:

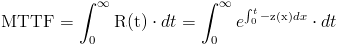
Una de las propiedades de la distribución exponencial es que la tasa de fallos es constante, por lo tanto:

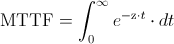
Realizamos el cambio de variable:

· x = -z·t
· dx = -z·dt

Y seguimos operando:

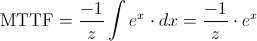
Deshacemos el cambio de variable:

· x = -z·t

Y, finalmente obtenemos:

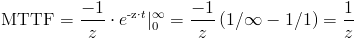
Por lo tanto, la tasa de fallo de la unidad expuesta por el enunciado es:

· Z(t) = 1/1000 = 0.001.

La fiabilidad del sistema en serie compuesto por diez elementos idénticos es el producto de cada uno de ellos:

R(t) = R₁(t) ··· R₁₀(t) = [R(t)]¹⁰ = [e^-(1/1000)·t]¹⁰ = e^-(1/100)·t

Por lo tanto, la función de fiabilidad del sistema es:

R_I(t) = e^-0.01·t

El enunciado nos indica que se conecta una unidad, con las mismas características de las anteriores,en paralelo al sistema formado por 10 unidades en serie.

Obtenemos la función de fiabilidad del nuevo sistema completo:

R(t) = 1 - (1 - R_I)·(1 - R₁) = 1 - (1 - e^-0.01·t)·(1 -e^-0.001·t) = 1 - (1 - e^-0.01t - e^-0.001t + e^-0.011t)

Simplifico y obtengo la función de fiabilidad del sistema compuesto por las diez unidades en serie con la unidad en paralelo:

R(t) = e^-0.01t + e^-0.001t - e^-0.011t

Ahora soy capaz de calcular la fiabilidad a las 50 horas de funcionamiento:

R(50) = e^-0.01·50 + e^-0.001·50 - e^-0.011·50 ≈ 0.980810

Podemos observar por el resultado, que es una fiabilidad alta.

Todavía no hemos terminado de resolver este problema, ya que nos piden obtener la tasa de fallos del sistema completo (las diez unidades en serie con la unidad en paralelo), para ello, necesitamos saber antes, la expresión de la función de probabilidad:

f(t) = F'(t) = [1 - R(t)]' = [-R(t)]'

Operamos:

f(t) = -[e^-0.01t + e^-0.001t - e^-0.011t]' = -[-0.01e^-0.01t - 0.001e^-0.001t + 0.011e^-0.011t]

Por lo tanto, la función de probabilidad es:

f(t) = 0.01e^-0.01t + 0.001e^-0.001t - 0.011e^-0.011t

Ahora, podemos calcular la tasa de fallos para cualquier instante de tiempo de fallo, por definición:

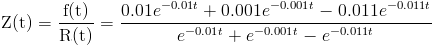
La tasa de fallos a las 50 horas es:

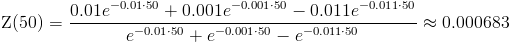
Podemos observar fácilmente que la tasa de fallo del sistema (diez elementos en serie en paralelo con un elemento, todos idénticos) no es constante, sino que varía para distintos instantes de tiempo de fallo, t.