Problema18: Fiabilidad

Ej18. Un sistema está constituido por dos unidades A y B conectadas en serie cuyas tasas de fallo son:

· Z_A(t) = 0.003·t^0.2
· Z_B(t) = 0.001

Teniendo ne cuenta que t está expresado en horas, determinar:

a) La fiabilidad de ambas unidades y la fiabilidad del sistema.

b) ¿Cuál es la tasa de fallo del sistema?.

c) Halle la probabilidad de que el sistema falle antes de 100 horas, suponiendo que lleva 300 horas en funcionamiento. ¿Tiene el dispositivo la propiedad de carencia de memoria?.

d) Para aumentar la fiabilidad, se conecta en paralelo con la unidad B, otra unidad idéntica a B, ¿cuál es ahora la fiabilidad del sistema? Demuestre que al cabo de mucho tiempo, la fiabilidad del sistema modificado tiende a ser el doble de la del sistema original.


Apartado a)

Nos piden obtener la función de fiabilidad de cada unidad.

· Función de Fiabilidad de la Unidad A:

Empleamos la expresión matemática de la función de fiabilidad:

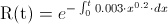
Operando:

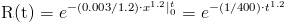
· Función de Fiabilidad de la Unidad B:

Empleamos la expresión matemática de la función de fiabilidad:

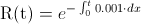
Operando:

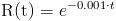
· Función de Fiabilidad del Sistema:

Al estar las unidades A y B en serie, la fiabilidad del sistema es el producto de la fiabilidad de cada unidad:

Apartado b)

En este apartado nos piden obtener la tasa de fallos del sistema completo, para ello, necesitamos saber antes, la expresión de la función de probabilidad:

f(t) = F'(t) = [1 - R(t)]' = [-R(t)]'

Operamos:

f(t) = -[e^{-(0.001t + (1/400)t1.2)}]' = (0.001 + (1.2/400)·t^0.2)·e^{-(0.001t + (1/400)t1.2)}

Ahora, podemos calcular la tasa de fallos para cualquier instante de tiempo de fallo, por definición:

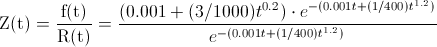
Simplificamos:

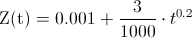
Podemos observar fácilmente que la tasa de fallo del sistema no es constante, sino que varía para distintos instantes de tiempo de fallo, t.


Apartado c)

Nos piden obtener la siguiente probabilidad:

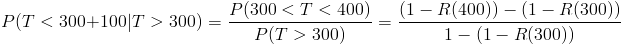
Simplificamos:

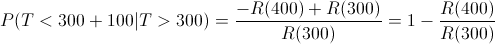
Y sustituimos valores:

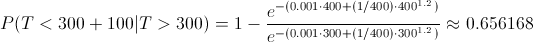
Si prestamos atención a la expresión de la probabilidad obtenida, ésta cambia de valor dependiendo del parámetro t, por lo tanto, no se cumple la propiedad de carencia de memoria (no es una distribución exponencial ni geométrica).


Apartado d)

El sistema que ahora nos ofrece este apartado es el siguiente:

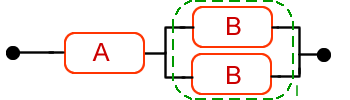
Los elementos B y B están en paralelo:

· R_I(t) = 1 - (1 - R_B)·(1 - R_B) = 1 - (1 - e^-0.001t)²

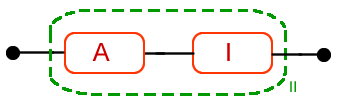
Los componentes A y I están en serie, por lo tanto, la fiabilidad del sistema es:

· R_II(t) = e^-(1/400)t1.2·[1 - (1 - e^-0.001t)²]

Nos piden que demostremos que al cabo de mucho tiempo, la fiabilidad del sistema modificado tiende ser a el doble del sistema original.

Vamos a desarrollar en la expresión de la fiabilidad del sistema modificado:

R_II(t) = e^-(1/400)t1.2·[1 - (1 - e^-0.001t)²] = e^-(1/400)t1.2·[1 - (1 - 2e^-0.001t + e^-0.002t)]

Simplificamos:

R_II(t) = e^-(1/400)t1.2·[1 - (1 - 2e^-0.001t + e^-0.002t)] = e^-(1/400)t1.2·[2e^-0.001t - e^-0.002t]

Por lo tanto:

R_II(t) = e^-(1/400)t1.2·[e^-0.001t·(2 - e^-0.002t)]

Podemos observar fácilmente que cuanto más grande sea t, el parámetro e^-0.002t es menos significativo que 2, por lo tanto, en el infinito:

R_II(∞) ≈ 2·e^{-(0.001t + (1/400)t1.2)}

Esto confirma que la fiabilidad del sistema modificado tiende a ser el doble del sistema original.