Problema17: Cartas de Control

Ej17. En un proceso productivo, los artículos fabricados se clasifican como defectuosos o no defectuosos, siendo ṗ la proporción media conocida de los primeros.

Para controlar dicho proceso, se utiliza una carta p, determinar:

a) ¿Cuál ha de ser el valor mínimo del tamaño muestral n, en función de ṗ, para que el límite inferior 3-sigma sea positivo?

b) Si ṗ = 0.2 y n = 64, halla los límites de control.

c) Con los datos del apartado anterior, ¿cuál es el LDP del proceso?.


Apartado a)

Debemos obtener el valor mínimo del tamaño muestral, en función de p, para que el límite de control inferior 3σ sea positivo.

El límite inferior 3σ viene definido por la expresión siguiente:

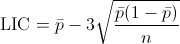
Dicho límite debe ser positivo:

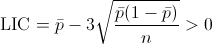
Despejo el parámetro ṗ:

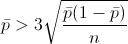
Opero y obtengo la solución a este apartado:

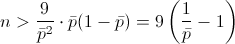
Apartado b)

En este apartado debemos obtener los límites de control 3σ de la carta de control p, los límites son:

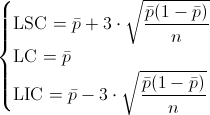
Donde:

· ṗ = 0.2
· n = 64

Sustituyo valores y obtengo la solución a este apartado:

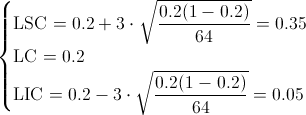
Apartado c)

En este apartado debemos obtener el LDP del proceso, definimos el evento:

· A ≡ Punto de la carta de control que queda fuera de los límites de control 3σ.

La expresión del parámetro LDP es:

LDP = 1/P(A)

Debemos obtener la probabilidad de que un punto quede fuera de los límites de control 3σ:

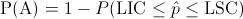
Teniendo en cuenta que:

·

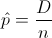
Siendo D, el número de unidades defectuosas en una muestra aleatoria de tamaño n. El evento D, sigue una distribución binomial: D ~ B(n, p).

Sustituimos:

P(A) = 1 - P(n·LIC ≤.D ≤.n·LSC)

Sustituimos valores:

P(A) = 1 - P(64·0.05 ≤.D ≤.64·0.35) = 1 - P(3.2 ≤.D ≤.22.4)

El evento D sólo es válido para números enteros positivos sin redondear, por lo tanto:

P(A) = 1 - P(3 ≤.D ≤.22)

Recordemos que el evento D sigue una distribución binomial: D ~ B(64, 0.2), comprobamos si se puede aproximar a la Normal:

· μ = n·p = 64·0.2 = 12.8 ≥ 5
· n = 64 > 25

Cumple con las condiciones necesarias para poder aproximar la binomial a la Normal, aplicamos el corrector por continuidad:

·

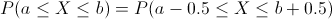
Por lo tanto, obtenemos:

· μ = n·p = 64·0.2 = 12.8
· σ = √(n·p·q) = √(64·0.2·(1-0.2) = 3.2

Tipificamos a la Normal teniendo en cuenta el corrector por continuidad:

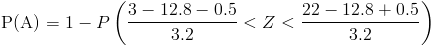
Aproximadamente es:

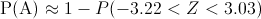
Simplificamos:

P(A) = 1 - [(0.5 + Φ(3.03)) - [1 - (0.5 + Φ(3.22))]] = 1 - Φ(3.03) - Φ(3.22)

Busco en la tabla de la Normal y obtengo la probabilidad de que un punto quede fuera de los límites de control 3σ:

P(A) = 1 - Φ(3.03) - Φ(3.22) = 1 - 0.4988 - 0.4994 = 0.0018

En estos momentos, disponemos de todos los datos necesarios para obtener el LDP:

LDP = 1/P(A) = 1/0.0018 ≈ 555.555556

Se necesitan, aproximadamente, 556 puntos para observar uno, fuera de los límites de control 3σ.