Problema19: Análisis de Regresión

Ej19. Un investigador considera que el salario que percibe un individuo es una función lineal de sus años de escolarización.

El investigador ha obtenido una muestra aleatoria de 100 individuos, de la que conocemos la siguiente información:

· Σx_i = 1000.
· ΣY_i = 1180.
· Σx²_i = 12820.
· ΣY²_i = 25543.
· Σx_i·Y_i = 13469.

Donde y_i, representa el salario mensual del individuo i, x_i los años de estudio de dicho individuo y.

Determinar:

a) Los coeficientes de regresión del modelo, así cómo el coeficiente de determinación. Interprete los resultados.

b) Obtenga un intervalo de confianza del 95% para el parámetro β₁.

c) ¿Es significativa la regresión lineal a un nivel de significación de 0.05? ¿Existe alguna contradicción con el valor calculado del coeficiente de determinación?


El enunciado del problema nos ofrece, esta vez, los datos resumidos y necesarios para realizar el estudio que nos plantea.


Aparatdo a)

Para calcular la pendiente, la expresión matemática es:

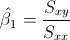
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:

·

·

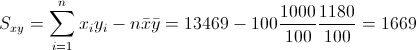
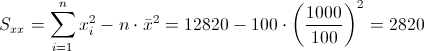
Por lo tanto, la pendiente es:

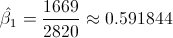
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada:

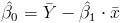
Sustituimos valores:

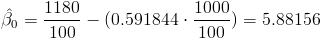
Por lo tanto, la ecuación de regresión ajustada es:

Y(x) = 5.88156 + 0.591844·x

Para obtener el coeficiente de determinación, empleamos su expresión matemática:

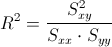
Debemos obtener el valor de Syy:

·

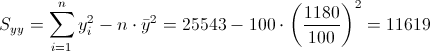
Sustituimos valores y obtenemos el resultado del coeficiente de determinación:

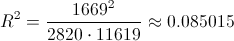
Al no estar próximo a 1, la regresión no es significativa ya que la variabilidad entre ambas variables no es, para nada, buena.

Hay que tener en cuenta que, el coeficiente de determinación mide la proporción de variabilidad total de la variable dependiente y, respecto a su media que es explicada por el modelo de regresión.


Apartado b)

En este apartado nos piden obtener un intervalo de confianza para el parámetro β1, cuya expresión matemática es:

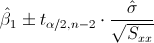
Al 95%, obtenemos α:

100(1 - α) = 95

Despejamos el parámetro que nos interesa: α = 0.05.

Debemos obtener el valor del estimador de la desviación estándar:

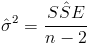
Siendo:

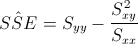
Tenemos todos los datos necesarios, calculados en apartados anteriores, para estimar la varianza:

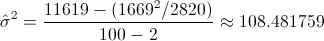
Por lo tanto, para un nivel de significación de: α = 0.05:

· t_{α/2, n -2} = t_{0.05/2, 100 -2} = t_{0.025, 98}

En la tabla t-Student, no existe el grado de libertad 98, por lo que realizamos una interpolación lineal para obtener un valor aproximado:

..90...........98.......120
1.9867.......P.......1.9799

De donde:

90 - 120.-> 1.9867 - 1.9799
90 - 98.-> 1.9867 - P

Calculamos:

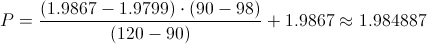
Sustituimos valores en la expresión del intervalo de confianza para el parámetro de la pendiente:

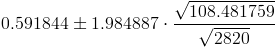
Por lo tanto, el intervalo de predicción al 95% es:

[0.202539, 0.981149]

Apartado c)

Para estudiar si la regresión es significativa, la pendiente debe ser distinta de cero. Calcularemos la región crítica.

La prueba de hipótesis es:

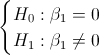
El estadístico es:

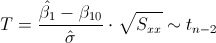
Obtenemos el valor del estadístico:

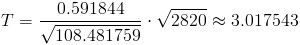
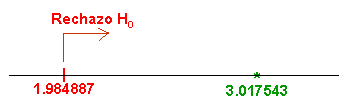
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

|T| > t_{α/2, n -2}

Para un nivel de significación de: α = 0.05, tenemos, en la tabla t-Student:

· t_{α/2, n -2} = t_{0.05/2, 100 -2} = t_{0.025, 98} ≈ 1.984887

Comprobamos el valor del estadístico con la región crítica:

Se cumple la condición de la región crítica, por lo tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa.

Esto quiere decir que, la pendiente no vale cero, por lo tanto, existen evidencias significativas de regresión lineal.

No es que exista contradicción con el valor del coeficiente de determinación, sino que dicho coeficiente nos da información sobre la variabilidad entre las variables del modelo, y según lo calculadao, no es buena.

Y la prueba de hipótesis que hemos realizado en este apartado, nos anuncia que la pendiente del modelo obtenido no es nula, por lo que existe regresión lineal, pero entre las variables, la relación o dependencia lineal, no es buena.