Ej18. Se requiere realizar un análisis rápido de la concentración de una sustancia en una cierta disolución mediante lecturas dadas por un colorímetro.
Para ello se determinaron cuidadosamente las concentraciones, x (mg/cm3), de la sustancia en otras tantas disoluciones, anotándose las lecturas y, correspondientes al colorímetro:
| x. | 42 | 170 | 275 | 330 | 390 | 410 |
| y | 90 | 48 | 61 | 69 | 80 | 89 |
Determinar:
a) Si la concentración es de 48 mg/cm3, ¿que lectura del colorímetro se puede predecir considerando una dependencia lineal entre las variables? ¿Crees que es aceptable el ajuste realizado?
b) Construye un intervalo de confianza al 95% para la pendiente de la recta de regresión. A la vista de este resultado, ¿puede decirse que la regresión es significativa?.
Antes de empezar a resolver los apartados propuestos, hacemos una recopilación de datos que podemos extraer de la tabla dada, ya que posteriormente serán de gran utilidad.
· n = 6
·
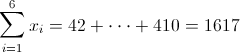
·
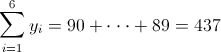
·
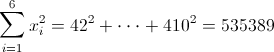
·
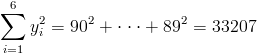
·
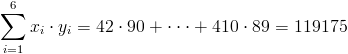
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
En este apartado nos piden varias cosas, lo primero que haremos es, obtener una recta lineal ajustada mediante el método de los mínimos cuadrados, ya que nos indican que consideremos una dependencia lineal entre las variables.
Para calcular la pendiente, la expresión matemática es:
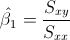
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:
·
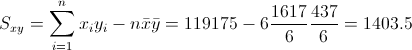
·
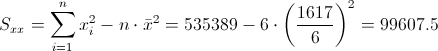
Por lo tanto, la pendiente es:
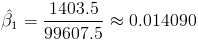
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada:
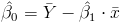
Sustituimos valores:
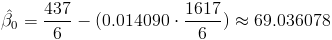
Por lo tanto, la ecuación de regresión ajustada es:
y(x) = 69.036078 + 0.014090·x
Una vez obtenido el modelo lineal, vamos a comprobar que valor nos daría el colorímetro con una concentración de 48mg/cm3:
y(48) = 69.036078 + 0.014090·48 = 69.712398
Para ver si realmente el ajuste es bueno, vamos a calcular el coeficiente de determinación, empleamos su expresión matemática:
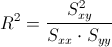
Debemos obtener el valor de Syy:
·
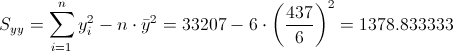
Sustituimos valores y obtenemos el resultado del coeficiente de determinación:
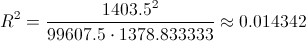
Al no estar próximo a 1, la calidad de ajuste es mala, es decir, no existen evidencias significativas en afirmar que existe dependencia lineal entre las variables.
Por lo tanto, el ajuste realizado es no aceptable.
Por lo tanto, el ajuste realizado es no aceptable.
Apartado b)
En este apartado nos piden obtener un intervalo de confianza para la pendiente de la recta de regresión, cuya expresión matemática es:
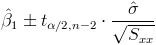
Al 95%, obtenemos α:
100(1 - α) = 95
Despejamos el parámetro que nos interesa: α = 0.05, tenemos, en la tabla t-Student:
· tα/2, n -2 = t0.05/2, 6 -2 = t0.025, 4 = 2.7765
Debemos obtener el valor del estimador de la desviación estándar:
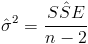
Disponemos de todos los datos, calculados en el apartado anterior, necesarios para estimar la varianza:
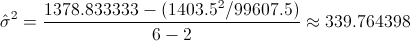
Sustituimos valores en la expresión del intervalo de confianza para la pendiente:
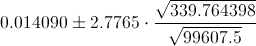
Por lo tanto, el interválo para la pendiente de la recta de regresión, al 95% es, aproximadamente:
[-0.148069, 0.176249]
Al contener el valor cero el intervalo de confianza, podemos afirmar que no es significativa la regresión lineal para el propuesto nivel de significación.





3 comentarios:
En la tabla de datos los 2 primeros están al contrario!!
Y una vez hecho el cambio, los datos de la x corresponden a la Y y viceversa. Esto sería necesario para que coincidiese con la solución!!gracias!!
Buenas Jaimes:
En este ejercicio no se lo que ha pasado que incluso al recopilar los datos los he mezclado.
Ya están recogidos y revisado el problema, aún así, te pongo la solución en R:
> x <-c(42,170,275,330,390,410)
> y<-c(90,48,61,69,80,89)
> summary(lm(y~x))
Call:
lm(formula = y ~ x)
Residuals:
1 2 3 4 5 6
20.372 -23.431 -11.911 -4.686 5.469 14.187
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 69.03600 17.44625 3.957 0.0167 *
x 0.01409 0.05840 0.241 0.8212
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 18.43 on 4 degrees of freedom
Multiple R-squared: 0.01434, Adjusted R-squared: -0.2321
F-statistic: 0.0582 on 1 and 4 DF, p-value: 0.8212
Dónde lo más significativo está en el valor de los coeficientes, que se puede comprobar que ya están correctos.
Disculpas por los errores, a veces el estructurar y la escritura en LaTex se vuelve tediosa a la hora de componer una entrada.
Gracias por avisarme y por tu comentario, un saludo.
Publicar un comentario