Problema16: Cartas de Control

Ej16. La siguiente lista representa el número de defectos de soldadura observados en 24 muestras de cinco tarjetas de circuito impreso cada una:

7...

6.

8.

10..

24.

6.

5.

4.

8.

11.

15.

8.

4.

16.

11.

12.

8.

6.

5.

9.

7

14..

8..

21

Determinar:

a) Los límites de una carta de control para el número de defectos. ¿Está el proceso bajo control?

b) Los límites de una carta de control para el número de defectos por unidad. ¿Está el proceso bajo control?


Apartado a)

Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:

· Carta de control C, número de defectos.
· Tamaño de la muestra: n = 5.
· Número de muestras: m = 24.

Nos piden obtener la carta de control del número de defectos, C, cuyos límites de control son:

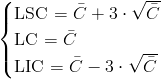
Siendo:

·

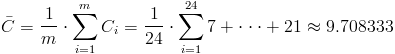
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de defectos, C:

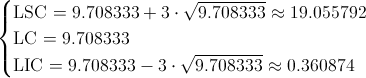
Vamos a representar gráficamente el proceso que estamos estudiando.

Para ello, debemos obtener los límites σ y 2σ de la misma, para su posterior análisis mediante el método: Western Electric Handbook 1956.

Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.

En este caso, usaremos la regla de tres para obtener los límites de control de advertencia.

- Para el límite superior:

(LSC - LC)/3 = (19.055792 - 9.708333)/3 ≈ 3.115820

Por lo tanto, los límites de advertencia de control 2σ son:

· c + 2·σ = 9.708333 + 2·3.115820 = 15.939973

Para los límites de advertencia de control σ son:

· c + σ = 9.708333 + 3.115820 = 12.824153

- Para el límite inferior:

(LC - LIC)/3 = (9.708333 - 0.360874)/3 ≈ 3.115820

Por lo tanto, los límites de advertencia de control 2σ son:

· c - 2·σ = 9.708333 - 2·3.115820 = 3.476693

Para los límites de advertencia de control σ son:

· c - σ = 9.708333 - 3.115820 = 6.592513

Podemos comprobar, que tanto para el límite superior como para el inferior, el valor es el mismo, esto es así ya que existe la misma distancia entre la línea central, LC, con el límite superior, LSC, y el límite inferior, LIC.

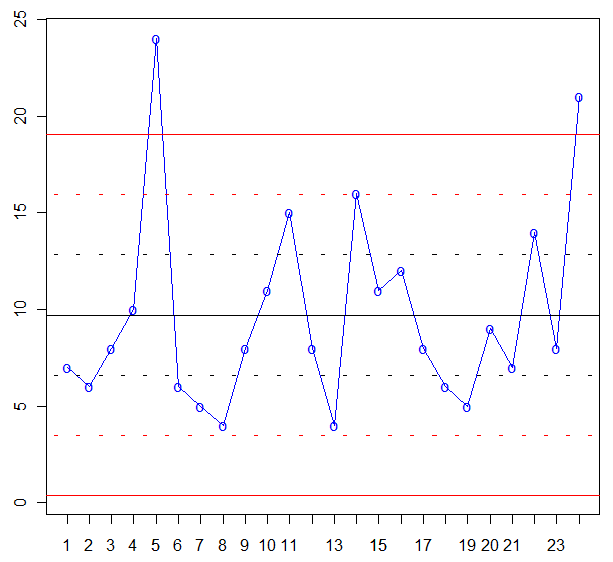
Y en este momento, estamos en disposición de realizar la gráfica de control C:

Una vez dibujada la gráfica de control, pasamos a su análisis. En un primer vistazo observamos que dos puntos, el número 5 y el 24, están fuera de los límites de control 3σ, por lo tanto, el proceso está fuera de control.


Apartado b)

Realizamos una recopilación de los datos ofrecidos por el enunciado del problema:

· Carta de control U, número de defectos por unidad.
· Tamaño de la muestra: n = 5.
· Número de muestras: m = 24.

Nos piden obtener la carta de control del número de defectos por unidad, U, cuyos límites de control son:

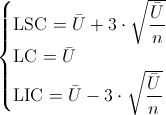
Siendo:

·

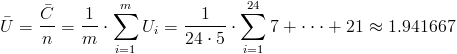
Ya disponemos de todos los datos necesarios para obtener los límites de control de la carta de defectos por unidad, U:

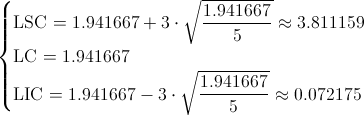
Debemos representar la carta de control U, del número de defectos por unidad, pero antes, debemos obtener los límites σ y 2σ de la misma, para su posterior análisis mediante el método: Western Electric Handbook 1956.

Para obtener los límites de advertencia σ y 2σ, existen dos formas, una es mediante una simple regla de tres, y la otra, algo más sofisticada, es obteniendo el valor de σ.

En este caso, usaremos la regla de tres para obtener los límites de control de advertencia.

- Para el límite superior:

(LSC - LC)/3 = (3.811159 - 1.941667)/3 = 0.623164

Por lo tanto, los límites de advertencia de control 2σ son:

· u + 2·σ = 1.941667 + 2·0.623164 = 3.187995

Para los límites de advertencia de control σ son:

· u + σ = 1.941667 + 0.623164 = 2.564831

- Para el límite inferior:

(LC - LIC)/3 = (1.941667 - 0.072175)/3 = 0.623164

Por lo tanto, los límites de advertencia de control 2σ son:

· u - 2·σ = 1.941667 - 2·0.623164 = 0.695339

Para los límites de advertencia de control σ son:

· u - σ = 1.941667 - 0.623164 = 1.318503

Podemos comprobar, que tanto para el límite superior como para el inferior, el valor es el mismo, esto es así ya que existe la misma distancia entre la línea central, LC, con el límite superior, LSC, y el límite inferior, LIC.

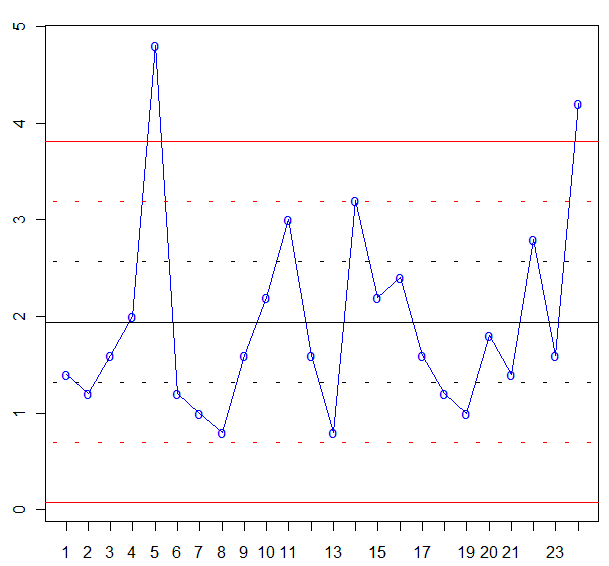
Y en este momento, estamos en disposición de realizar la gráfica de control U:

Una vez dibujada la gráfica de control, pasamos a su análisis. En un primer vistazo observamos que dos puntos, el 5 y el 24, están fuera de los límites de control 3σ, por lo tanto, el proceso está fuera control