Ej17. Un sistema paralelo está formado por 10 unidades idénticas e independientes, cada una con una distribución de Weibull del tiempo de fallo, de parámetro β = 72.
Determinar:
a) El valor del parámetro α, sabiendo que la probabilidad de que el sistema falle antes del instante t = 36, es 0.601.
b) ¿En qué instante la tasa de fallo de un sistema serie formado por 10 unidades como las anteriores, será 2.5?
Recopilamos información útil que nos ofrece el enunciado del problema:
· Sistema Paralelo: 10 Unidades iguales.
· Todas las unidades siguen una distribución de Weibull: W(α, 72).
La función de fiabilidad de la distribución de Weibull viene dada por la siguiente expresión:
R(t) = e-tα/β
Donde:
· α ≡ Parámetro de forma.
· β ≡ Parámetro de escala.
En nuestro caso, sustituyendo valores:
· Una única unidad: R1(t) = e-tα/72
Lo primero que haremos, es obtener la función de fiabilidad para cualquier instante de tiempo de fallo del sistema global compuesto por 10 unidades:
R(t) = 1 - (1 - R1(t))·(1 - R2(t))·(1 - R3(t))····(1 - R10(t)) = 1 - (1 - e-tα/72)10
Pasamos a resolver los distintos apartados que nos ofrece el problema.
Apartado a)
En este apartado nos piden calcular el parámetro de forma, α, para el instante de tiempo t = 36, dándonos el valor de la función de distribución acumulada, en este caso: F(36) = 0.601.
Pues bien, con todos estos datos, estamos capacitados para resolver este apartado:
F(t) = 1 - R(t) = 0.601
Operamos:
R(t) = 1 - 0.601 = 0.399
Sustituimos el valor de R(t) del sistema:
1 - (1 - e-36α/72)10 = 0.399
Despejamos:
e-36α/72 = 1 - 10√0.601
Aplicamos logaritmo neperiano:
-36α/72 = Ln(1 - 10√0.601)
Seguimos operando:
36α = -72·Ln(1 - 10√0.601)
Y volvemos aplicar logaritmo neperiano:
α·Ln(36) = Ln[-72·Ln(1 - 10√0.601)]
Y por fin, despejamos el parámetro requerido, parámetro de forma:
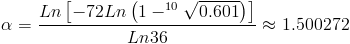
Por lo tanto, el parámetro de forma, para los datos dados tiene el valor de, aproximadamente, 1.500272.
Apartado b)
En este apartado, el sistema está formado por 10 unidades idénticas en serie, vamos a obtener la función de fiabilidad para cualquier instante de tiempo de fallo del sistema global:
R(t) = R1(t)·R2(t)·R3(t)····R10(t) = (e-tα/72)10 = e-10tα/72
Pero antes, necesitamos saber la expresión de la función de probabilidad:
f(t) = F'(t) = [1 - R(t)]' = [-R(t)]' = -[e-10tα/72]' = (15.00272/72)·t0.500272·e-10t1.500272/72
Ahora, podemos calcular la tasa de fallos para cualquier instante de tiempo de fallo, por definición:
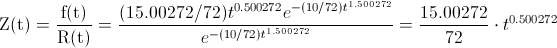
Nos indican que la tasa de fallos vale 2.5, por lo tanto:
(15.00272/72)·t0.500272 = 2.5
Despejamos:
t0.500272 = (2.5·72)/15.00272
Aplicamos logaritmo neperiano:
0.500272Ln(t) = Ln[(2.5·72)/15.00272]
Despejamos:
Ln(t) = Ln[(2.5·72)/15.00272]/0.500272
Y por fin, despejamos la variable deseada, t, obteniendo la solución a este apartado:
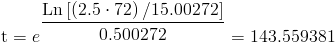
Por lo tanto, el instante en que la tasa de fallo tiene valor 2.5 es 143.559381.
2 comentarios:
en el apartado b) para calcular la Z(t) del sistema completo, ha utilizado la fiabilidad de una de las unidades no??
en tal caso, para obtener la tasa de fallo del sistema completo, habria que, o bien multiplicar su resultado por 10 (si empleamos la fiabilidad de una unidad) o bien derivar la fiabilidad del sistema, i.e., la que ha empleado elevado a 10....
creo que la primera opcion es mas sencilla, pero tengo entendido que el dar por hecho que la tasa de fallo de un sistema en serie es igual al sumatorio esta mal, y habria que demostrar que es cierto (algo que supongo que no sera facil).
espero no haberme equivocado.
un saludo y gracias por su esfuerzo, a muchos nos es muy util
Buenas:
Tu comentario es algo confuso, creo que no tienes los conceptos claros de sistema en serie y sistema en paralelo.
En un sistema en serie, como es el que este problema propone, la función de fiabilidad o de supervivencia del sistema en completo es el producto de todas las funciones de fiabilidad de los elementos que componen dicho sistema en serie, jamás el sumatorio de los elementos.
Una de las propiedades de los sistemas en serie es que su función de fiabilidad total del sistema es inferior a la unidad de mayor fiabilidad que componen el sistema.
Y la tasa de fallos, pues es tal y como se indica en el apartado b), se obtiene la función de probabilidad del sistema y se divide por la función de fiabilidad del sistema, así se obtiene la tasa de fallos del sistema completo.
La demostración del porqué de la función de fiabilidad de un sistema en serie o paralelo creo recordar que está resuelta en uno de los ejemplos de este capítulo, aún así, no es difícil obtenerla.
PD: Perdona por el retraso pero he estado de mini vacaciones.
Un saludo y gracias por tu comentario.
Publicar un comentario