Ej14. Los datos reflejados en la siguiente tabla relacionan los niveles de concentración de una sustancia, presentes en 6 muestras, con la respuesta observada en un colorímetro:
| x. | 4.2450 | 5.9480 | 12.8650 | 26.6660 | 35.1860 | 50.6510 |
| y | 0.0280 | 0.0440 | 0.0680 | 0.0920 | 0.1095 | 0.1295 |
El objetivo es encontrar una curva de calibración del tipo: y = α·xβ, que permita determinar la concentración a partir de la respuesta observada en el colorímetro.
Determinar el valor de α y de β.
NOTA: La variable x representa la respuesta del colorímetro y la variable y representa la concentración de la sustancia de la muestra.
El modelo que nos ofrece el problema no es un modelo lineal simple, por lo que tenemos que adecuarlo, en este caso, actuamos mediante logaritmo neperiano:
Ln(y) = Ln(α·xβ) = Ln(α) + β·Ln(x)
Cambio de Variable:
¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨
· y* = Ln(y)
· x* = Ln(x)
· b0 = Ln(α)
El modelo ajustado, con el cambio de variable, es:
Y la tabla quedará tal y como sigue:
| x**. | Ln(4.2450) | Ln(5.9480) | Ln(12.8650) | Ln(26.6660) | Ln(35.1860) | Ln(50.6510) |
| y* | Ln(0.0280). | Ln(0.0440). | Ln(0.0680). | Ln(0.0920). | Ln(0.1095) | Ln(0.1295) |
Ahora, podemos hacer una recopilación de datos que se extraen de la tabla una vez realizado el cambio de variable.
· n = 6
·
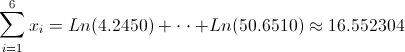
·
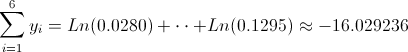
·
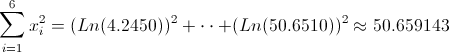
·
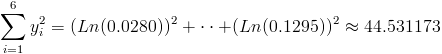
·
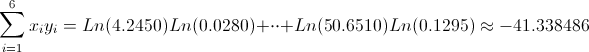
Para calcular la pendiente, la expresión matemática es:
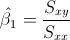
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:
·
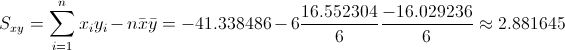
·
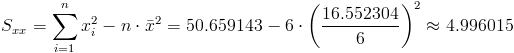
Por lo tanto, la pendiente es:
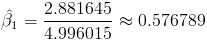
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada. Sustituimos valores:
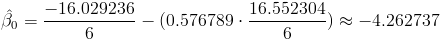
Por lo tanto, la ecuación de regresión ajustada es:
y*(x*) = -4.262737 + 0.576789·x*
Siendo:· y* = Ln(y)
· x* = Ln(x)
· b0 = Ln(α) = -4.262737
· b1 = β = 0.576789
El modelo no lineal quedará:
Siendo:
· α = e-4.262737 ≈ 0.014084
· α = e-4.262737 ≈ 0.014084





5 comentarios:
Buenas, tenía una pregunta sobre este ejercicio:
Ln(y) = Ln(α·x^β) = Ln(α) + β·Ln(x) no debería ser:
Ln(y) = Ln(α·e^xβ) = Ln(α) + β·Ln(x)tal y como define el ejercicio. Gracias
Buenas:
Tienes razón, según el enunciado del problema debería ser tal y como dices.
Ya está corregido y actualizada la solución.
Un saludo y muchas gracias por el apunte.
Buenas de nuevo creo que la expresión que se busca es:
y = α·e^βx
ln(y)=ln(α·e^βx)
ln(y)=ln(α)+βxln(e)
ln(y)=ln(α)+βx
Un saludo y gracias.
Buenas:
Perdona por mi torpeza pero muchas veces, por falta de tiempo, me es imposible revisar los ejercicios en profundidad y es un tremendísimo error (y espero no volver a caer de nuevo).
Es cierto que la expresión de la curva dada no cumple no la resolución del problema, vamos hacer una cosa, y es cambiar la definición de la curva para así conservar la parte resolutiva del problema, ahora, la curva será la siguiente:
· y = α·x^β
De esta manera la parte de la solución es correcta. Por otro lado, me apunto el volver a realizar este mismo problema pero con la curva dada inicialmente (espero tenerlo publicado en una semana más o menos).
En caso de que quieras un ejercicio similar al inicial, el siguiente cumple con dichas especificaciones:
· Problema 8.
Un saludo y muchísimas gracias por el apunte.
Buenas:
Pues lo prometido es deuda, ya está publicado el problema con la curva dada inicialmente.
El ejercicio en cuestión es el siguiente:
· Problema 34.
Un saludo y perdón por las molestias.
Publicar un comentario