Ej22. La duración en días de un componente de un sistema de iluminación tiene una función de densidad cómo la que se muestra a continuación:
Con
· t > 0.
· α > 0.
Determinar:
a) La probabilidad de que un componente esté activo durante T días.
b) La probabilidad de que dure T días más si lleva funcionando 10 días.
c) Calcular la tasa de fallos.
d) Para un sistema concreto, se sabe que α = 0.003, obtener la probabilidad de que el sistema continúe funcionando a los 60 días si tiene 400 componentes en paralelo.
e) Calcular la probabilidad de que al acabar esos 60 días, continúen funcionando más de 4 componentes de esos 400.
Apartado a)
Para obtener la fiabilidad de que un componente esté activo durante T días, debemos, previamente calcular la función de fiabilidad genérica. Para ello, emplearemos la relación de la función de densidad y la función de fiabilidad:
R(t) = 1 - F(t)
Integrando la función de probabilidad entre 0 y t, obtenemos la función de densidad acumulada:
En esta función de fiabilidad debemos tener cuidado, ya que no es posible obtener una solución de manera directa, pero si realizamos un cambio de variable podemos resolverla sin mayores problemas.
Realizamos el cambio de variable:
· m = -α·t²/2
· dm = -α·x·dx
Sustituimos:
Deshacemos el cambio de variable:
· m = -α·t²/2
Y resolvemos para obtener la función de fiabilidad:
Apartado b)
Debemos obtener la siguiente probabilidad:
P(T > 10 + t | T > 10)
Al tener la función de fiabilidad, podemos resolver dicha probabilidad:
Apartado c)
La tasa de fallos es, por definición:
Vemos que la tasa de fallos no es constante para cualquier instante de t.
Apartado d)
En este apartado nos da un valor concreto para el parámetro α = 0.003 y nos dicen que se crea un sistema de 400 unidades idénticas de este componente en paralelo. Por lo tanto, la función de fiabilidad del sistema completo será:
RSISTEMA(t) = 1 - [1 - R(t)]⁴⁰⁰
Para obtener la fiabilidad a los 60 días, sustituimos valores:
Por lo tanto, la fiabilidad del sistema a que siga funcionando tras 60 días es de, aproximadamente 0.836464.
Apartado e)
Este apartado es un poco peculiar, ya que no sigue la temática del estudio y el uso de las expresiones de la fiabilidad, pero me parece interesante resolverlo ya que se puede ver, que la estadística es una herramienta muy potente en su conjunto.
Realizamos una recopilación de datos del apartado:
· X ≡ 'Nº de componentes que sigue funcionando a los 60 días'.
· La variable aleatoria X sigue una distribución Binomial: X ~ B(400, e⁻⁵'⁴)
· NOTA: La probabilidad de que un único componente siga funcionando a los 60 días es de:
Las características del tamaño de la muestra y la probabilidad relativamente baja que tiene, comprobaremos si podemos adaptar la distribución binomial a la de Poisson.
Para ello, debe cumplirse:
· n grande: n = 400 OK.
· n·p = 400·e⁻⁵'⁴ ≈ 1.806632 ≤ 7 OK.
Por lo tanto, se puede adaptar la variable aleatoria a la distribución de Poisson: X ~ P(1.806632).
La probabilidad que debemos obtener es la siguiente:
Al tener que calcularse el valor de varios elementos para obtener la solución a este apartado, vamos a emplear el software R para realizar dicha operación:
Para ello, debe cumplirse:
· n grande: n = 400 OK.
· n·p = 400·e⁻⁵'⁴ ≈ 1.806632 ≤ 7 OK.
Por lo tanto, se puede adaptar la variable aleatoria a la distribución de Poisson: X ~ P(1.806632).
La probabilidad que debemos obtener es la siguiente:
P(X > 4) = 1 - P(X ≤ 4) = 1 - [P(X = 0) + ··· + P(X = 4)]
Al tener que calcularse el valor de varios elementos para obtener la solución a este apartado, vamos a emplear el software R para realizar dicha operación:
>> ppois(c(4), 1.806632, lower.tail = F)
[1] 0.03688811
Por lo tanto, la probabilidad de que sigan funcionando más de cuatro componentes de entre 400 es de, aproximadamente 0.036888.


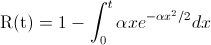
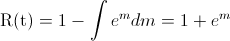
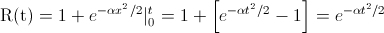
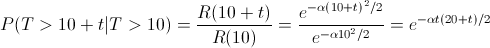
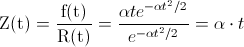
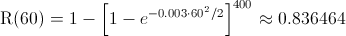
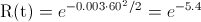




0 comentarios:
Publicar un comentario