Ej75. Una empresa de vigilancia instala un aparato electrónico que funciona de manera permanente. Su duración sigue una ley exponencial de 99.5 días de media. Al acabar cada día, se revisa el dispositivo y, en caso de que esté averiado, se sustituye por otro de similares características.
Determinar:
a) La probabilidad de que el aparato se estropee el primer día como máximo de funcionamiento.
b) ¿Cuál es la probabilidad de que se estropee en un día cualquiera si hasta el día anterior había funcionado correctamente?.
c) Calcular la probabilidad de que se estropee por primera vez a lo largo del día k+1.
Recopilamos los datos que nos ofrece el enunciado de este apartado:
· A ≡ 'Duración de un aparato de vigilancia en días'.
· Dicho suceso sigue una distribución exponencial, A ~ Exp(99.5) días.
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
Debemos emplear la función de distribución acumulada de la distribución exponencial:
La probabilidad que debemos obtener es la siguiente:
Apartado b)
En este apartado debemos obtener la siguiente probabilidad:
Hay que tener en cuenta que una de las propiedades fundamentales de la distribución exponencial es que carece de memoria, por lo tanto:
La solución a este apartado ya se ha obtenido en el anterior, es de, aproximadamente, 0.01.
Apartado c)
En este apartado debemos obtener la siguiente probabilidad:
Empleamos la función de distribución acumulada para resolverla:
Operamos y obtenemos la solución a este apartado:
¿De qué manera? Te lo muestro operando la expresión anterior:
Hacemos un cambio de variable:
· p ≡ e-1/99.5
Por lo tanto, nos queda:

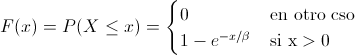




0 comentarios:
Publicar un comentario