Ej88. Se desea vigilar un recinto cerrado, y para tal fin, una empresa de vigilancia ha instalado un total de 25 aparatos de vigilancia, de los que 6 tienen carcasa roja y 19 negra. En el periodo de revisión diaria, no hay equivocaciones si el dispositivo se ha estropeado pero, a veces, se retira uno que funciona adecuadamente.
La probabilidad de confundirse es de 0.06 entre los de color rojo y 0.07 entre los negros.
Calcular la probabilidad de que no funcione un aparato que ha sido retirado.
Realizamos una recopilación de datos dados por el enunciado del problema:
· R ≡ 'Aparatos de vigilancia con carcasa roja'.
· N ≡ 'Aparatos de vigilancia con carcasa negra'.
· P(R) = 6/25.
· P(N) = 19/25.
· S ≡ 'Sustituir aparato de vigilancia'.
· E ≡ 'Dispositivo estropeado'.
· P(S|E) = 1.
· P(S|(Ē ∩ R)) = 0.06.
· P(S|(Ē ∩ N)) = 0.07.
Nos piden obtener la probabilidad de que no funcione un dispositivo que ha sido retirado, emplearemos para tal fin la Ley de Bayes:
Para resolver el problema, debemos obtener antes la probabilidad de sustituir un dispositivo, para ello, aplicamos la Ley de Probabilidad Total:
Sustituimos valores:
Ya disponemos de todos los valores necesarios para obtener la solución del problema:
Por lo tanto, la probabilidad de que no funcione un dispositivo ha sido retirado es de, aproximadamente 0.129998.

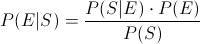
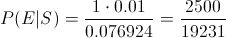




1 comentarios:
Buenas
una pregunta, ¿no es demasiado pequeña la probabilidad?, es decir el enunciado te dice que la probabilidad de retirar una que no este realmente estropeado es muy chica, o sea que la probabilidad de retirar uno estropeado debería ser mas alta.
Publicar un comentario