Ej76. Una empresa ha diseñado una alarma que avisa hasta con una hora de anticipación de que se va a producir un fallo. El tiempo de adelanto, expresado en horas, en el que salta la alarma tiene como función de densidad:
f(x) = 3x² , para 0 ≤ x ≤ 1.
Si ya ha pasado un cuarto de hora desde que sonó la alarma y no se ha producido el fallo, ¿qué probabilidad hay de que haya sonado con menos de media hora de antelación?
Antes de resolver nada, obtendremos la función de distribución acumulada que nos será muy útil para obtener cualquier probabilidad.
En nuestro caso, el intervalo que tenemos que realizar cálculos es: 0 ≤ x ≤ 1:
Por lo tanto, la función de distribución acumulada queda tal y como se muestra a continuación:
Una vez obtenida la función de distribución acumulada, podemos calcular cualquier probabilidad, en nuestro caso:
Por lo tanto, la probabilidad de que haya sonado con menos de media hora de antelación habiendo pasado ya un cuarto de hora es de, aproximadamente 0.111111.

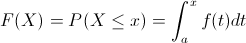
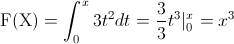
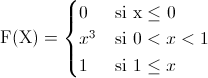
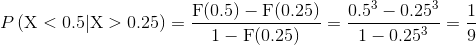




2 comentarios:
la probabilidad calculada fue P(X<0.5/X>0.25) , favor arreglar esto, me generó una gran confusión y puede que a otros también.
gracias por su página.
Buenas:
Ya está subsanado, te pido disculpas por la confusión que te pudo generar.
Gracias por tu comentario, un saludo.
Publicar un comentario