Ej20. El número de defectos superficiales en una cinta magnética, tiene una distribución de Poisson con una media de 0.2 defectos por metro de cinta. Sea X la distancia entre dos defectos consecutivos.
Determinar:
a) La esperanza de X.
b) La probabilidad de que no existan defectos en 10 metros consecutivos de cinta magnética. ¿Cambia la respuesta si los 10 metros no son consecutivos?
c) Calcula los metros de cinta que son necesarios revisar para que la probabilidad de encontrar al menos un defecto sea 0.9.
d) Calcula la probabilidad de que la primera vez que se encuentre que una distancia entre dos defectos es mayor que 8 metros, se presente en el quinto defecto.
Realizamos una recopilación de datos del enunciado del problema:
· X ≡ 'Distancia entre dos defectos consecutivos'.
· La variable aleatoria X sigue una distribución de Poisson: X ~ P(0.2) defectos por metro de cinta.
Pasamos a resolver los distintos apartados que nos ofrece el problema.
Apartado a)
Como la variable aleatoria X sigue una distribución de Poisson, la esperanza es:
· E(X) = λ = 0.2
Por lo tanto, 0.2 serán los defectos esperados por metro de cinta.
Apartado b)
Si una cinta magnética contiene 10m, adaptamos la variable a estas especificaciones:
· Variable aleatoria X con 10m: X ~ P(10·0.2) = P(2).
La probabilidad que nos piden obtener es la siguiente:
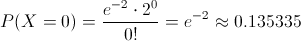
Por lo tanto, la probabilidad de que no encontremos ningún defecto en una cinta magnética con 10m es de 0.135335.
Y a la pregunta si cambia el valor de probabilidad si los defectos son consecutivos o no, la respuesta es no, la probabilidad es la misma ya sean defectos consecutivos o salteados.
Apartado c)
En este apartado, nos piden obtener la cantidad de metros necesarios en la cinta magnética para que la probabilidad de encontrar, al menos, un defecto sea 0.9.
Por lo tanto:
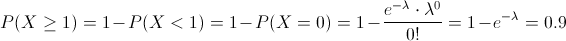
Despejamos:
Resolvemos la igualdad empleando las propiedades del logaritmo neperiano:
Operamos:
Por metro:
Por lo tanto, los metros necesarios para encontrar al menos un defecto sea 0.9 son 11.512925 metros.
Apartado d)
Para este apartado, la variable aleatoria sigue una distribución geométrica, X ~ G(0.2), por lo tanto, nos piden obtener la probabilidad siguiente:





8 comentarios:
por que en el calculo de la E(X) = 1/λ = 1/0.2 = 5?
si en la parte de teoria dice que la E(X)= λ?
no estoy seguro de entender pero lo que pide es la cant de defectos y no la probabilidad de que los haya por metro?
gracias! el blog esta increible y me ayuda muchisimo.
tengo un modelo de parcial con este mismo ejercicio ademas! por eso quiero entenderlo bien.
saludos
Buenas @andres:
Tienes razón, la esperanza matemática de una distribución de Piosson es su propio parámetro, supongo que me equivoqué con la distribución Geométrica.
Con respecto a la segunda pregunta, ¿a qué apartado te refieres? No la entiendo.
Supongo que te refieres al tercer apartado, dónde nos piden los metros necesarios dada una probabilidad.
Para tal fin, obtenemos el parámetro de la Poisson y después, teniendo en cuenta los detalles de la propia cinta, obtenemos los metros necesarios.
Un saludo y me alegro de que te sirva el contenido que aquí exponemos.
hola! en el apartado de mayor que 8 metros no interviene?? daria igual que me pregunten:"Calcula la probabilidad de que la primera vez que se encuentre que una distancia entre dos defectos es mayor que 9 metros, se presente en el quinto defecto." por que?
GRACIAS!!
Buenas:
¡Cuidado! Tanto la distribución geométrica (variable aleatoria discreta) como la distribución exponencial (variable aleatoria continua), tienen la propiedad de carecer de memoria, en otras palabras, NO tienen memoria.
Un saludo.
Hola buenas, tengo una consulta
En el apartado d tomamos la media de poisson λ como la probabilidad del suceso que tenga exito en la formula de la distribucion geometrica, esta relacion entre uno y otro no la acabo de entender...si pudiera explicarmela se lo agredeceria
Saludos, Miguel Angel
Buenas Miguel Ángel:
No es que tengan una relación directa, más bien son dos problemas distintos en uno solo, es decir, mientras que los apartados a), b) y c) se basan en la Distribución de Poisson (tal y como se dice en el enunciado del problema), el último apartado, d), es diferente, éste apartado no sigue una Distribución de Poisson, sino una Distribución Geométrica.
Y es por ello que debemos pensar en términos de la Distribución Geométrica y recopilar los datos necesarios y útiles que el enunciado nos ofrezca, y en nuestro caso, tenemos la media de defectos que es justamente, el parámetro necesario para resolver el enunciado.
Un saludo.
Buenas.
En el apartado (d) no se utiliza el valor de 8mts que nos dan...o no encuentro donde se utiliza.
Si es verdad que no se usa ese dato de 8mts, que si afecta el resultado, entiendo mal planteado ese apartado?
Muchas gracias por tu blog y ayuda
Un saludo
Buenas:
La respuesta la tienes en los comentarios:
¡Cuidado! Tanto la distribución geométrica (variable aleatoria discreta) como la distribución exponencial (variable aleatoria continua), tienen la propiedad de carecer de memoria, en otras palabras, NO tienen memoria.
Está bien planteado el enunciado, ya que lo que quiere demostrar es que te has dado cuenta de que la distribución que debes usar es la Geométrica y que sabes usarla apropiadamente.
Un saludo.
Publicar un comentario