Problema28: VAD

Ej28. Si se seleccionan 13 cartas aleatoriamente (sin remplazamiento) de una baraja de 52 cartas, hallar la probabilidad de que:

a) 6 sean figuras.

b) Ninguna sea figura.


Realizamos una recopilación de datos del enunciado del problema:

· X ≡ 'Nº de figuras seleccionadas en una baraja de 52 cartas'.
· La variable aleatoria X sigue una distribución Hipergeométrica: X ~ HG de parámetros:
· Número total de cartas: N = 52.
· Tamaño de la muestra: n = 13. (Número total de cartas escogidas)
· Número total de figuras en la baraja de cartas: r = 12 (4 palos con 3 figuras dada uno).
· Número de figuras escogidas: x = x.

Pasamos a resolver los distintos apartados que nos ofrece el problema.


Apartado a)

Debemos hallar la siguiente probabilidad:

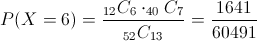
Por lo tanto, la probabilidad de escoger 6 figuras, es de 1641/60491.


Apartado b)

Para este apartado, debemos obtener la siguiente probabilidad:

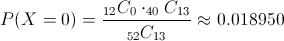
Por lo tanto, la probabilidad de escoger ninguna figuras, es de 0.018950.