Ej29. De 60 aspirantes a una universidad, 40 son del oriente. Si se seleccionan 20 aspirantes aleatoriamente, hallar la probabilidad de que:
a) 10 sean orientales.
b) No más de 2 sea orientales.
Realizamos una recopilación de datos del enunciado del problema:
· X ≡ 'Nº de personas, aspirantes a la universidad, que provengan de oriente'.
· La variable aleatoria X sigue una distribución Hipergeométrica: X ~ HG de parámetros:
· Número total de aspirantes a la universidad: N = 60.
· Tamaño de la muestra: n = 40. (Número total de orientales aspirantes a la universidad)
· Número total de seleccionados aleatoriamente: r = 20.
· Número de orientales escogidos: X = x.
Pasamos a resolver los distintos apartados que nos ofrece el problema.
Apartado a)
Debemos hallar la siguiente probabilidad:
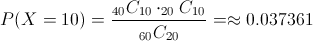
Por lo tanto, la probabilidad de seleccionar 10 orientales, es de 0.037361.
Apartado b)
Para este apartado, debemos obtener la siguiente probabilidad:
Sustituimos valores y obtenemos la solución a este apartado:
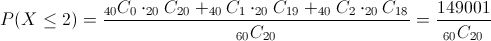
Que aproximadamente es:
Por lo tanto, la probabilidad de escoger menos o igual a dos orientales, es de 3.55·10-11, en otras palabras, muy poco probable.





3 comentarios:
parece que hubo un error en los datos n=20 y r=40
Buenas:
No hay error, la nomenclatura que se utiliza es la siguiente:
· N ≡ Número general de la muestra.
· n ≡ Número total dentro de N que se desea evaluar.
· r ≡ Número de seleccionados dentro de N que se desea evaluar.
Por propia definición, r siempre debe ser menor o igual a n.
Un saludo y gracias por tu comentario.
Si hay un error, n=20 y k o r=40, para que se cumpla n<=K o n<=N-k
Publicar un comentario