Ej37. Las proporciones de piezas defectuosas fabricadas por dos máquinas M1 y M2 son 0.04 y 0.01, respectivamente.
Se toma una pieza al azar y resulta aceptable. Sabiendo que la probabilidad de elegir una pieza de cualquiera de las dos máquinas es 0.5, calcular la probabilidad de que provenga de M1.
Realizamos una recopilación dados por el enunciado del problema:
· M1 ≡ 'Piezas fabricadas por la máquina M1'.
· M2 ≡ 'Piezas fabricadas por la máquina M2'.
· D ≡ 'Piezas defectuosas'.
· P(M1) = 0.5.
· P(M2) = 0.5.
· P(D|M1) = 0.04.
· P(D|M2) = 0.01.
En este problema, nos piden obtener la siguiente probabilidad (Ley de Bayes):
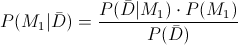
Obtengo previamente, la probabilidad de seleccionar una pieza defectuosa mediante la Ley de la Probabilidad Total:
P(D) = P(D|M1)·P(M1) + P(D|M2)·P(M2) = 0.04·0.5 + 0.01·0.5 = 0.025
El resultado que nos es válido es el complementario, la probabilidad de seleccionar una pieza que no sea defectuosa:
1 - 0.025 = 0.975
Ya disponemos de todos los datos necesarios para resolver este problema:
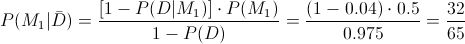
Por lo tanto, la probabilidad de que al sacar una pieza no defectuosa sea de la máquina M1 es de, aproximadamente, 0.492308.





2 comentarios:
Vale, lo he seguido bien, aunque con cierto esfuerzo. Mis nociones son bastante básicas (poco más que Laplace) pero con la explicación que das y lo poco que sé es facil de entender (y de aprender, por cierto) . Muy didáctico.
Buenas:
Este es un típico problema para aplicar la Ley de Bayes, donde previamente, se debe obtener la probabilidad de todas las piezas defectuosas, mediante la Ley de la Probabilidad Total.
Gracias por tu comentario y me alegra que te haya sido de utilidad.
Un saludo.
Publicar un comentario