Ej38. Un laboratorio quiere introducir en el mercado un test para detectar una enfermedad. Cuando la persona está enferma, el test indica un 95% de las veces que lo está. Sin embargo, a veces el test da positivo aunque la persona no tenga la enfermedad. Esto ocurre un 1% de las veces.
Si el 0.5% de la población está enferma, ¿cuál es la probabilidad de que una persona tenga la enfermedad cuando el test así lo indica?.
Realizamos una recopilación dados por el enunciado del problema:
· T ≡ 'Test para detectar una enfermedad'.
· E ≡ 'Persona que contiene la enfermedad'.
· P(E) = 0.005.
· P(T|E) = 0.95.
· P(T|Ē) = 0.01.
En este problema, nos piden obtener la siguiente probabilidad (Ley de Bayes):
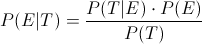
Obtengo previamente, la probabilidad de los resultados de realizar el test mediante la Ley de la Probabilidad Total:
P(T) = P(T|E)·P(E) + P(T|Ē)·P(Ē) = 0.95·0.005 + 0.01·(1-0.005) = 0.0147
En estos momentos, disponemos de todos los datos necesarios para resolver este problema:
Por lo tanto, la probabilidad de que una persona padezca la enfermedad cuando el test así lo indica es de, aproximadamente, 0.323129.
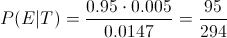
2 comentarios:
Buenas:
Cuando utilizas la ley de la probabilidad total para calcular P(T), ¿no deberían cubrirse todos los casos posibles? Ya que la suma de las probabilidades tanto si está enfermo como si no, 0.95+0.01=0.96 debería dar 1 al ser sucesos complementarios ¿no es así?
Les felicito por su blog, es muy completo y me es de mucha utilidad para estudiar esta disciplina, un saludo.
Buenas:
¡Cuidado! La suma de las probabilidades tanto si está enfermo como si no es el evento E, tú has sumado las probabilidades condicionales.
En otras palabras:
· P(E) + P(#E) = 0.005 + ( 1 - 0.005 ) = 1
Donde se demuestra que están presentes todos los casos.
Un saludo y gracias por tú comentario.
Publicar un comentario