Ej39. Tres máquinas A, B y C producen piezas con una proporción de defectuosas del 5%, 3% y 2% respectivamente. Se tiene un lote compuesto por 100 piezas de A, 50 de B y 50 de C.
Se extrae una pieza al azar. Determinar:
a) La probabilidad de que la pieza sea defectuosa.
b) Si la pieza es defectuosa, calcular la probabilidad de que venga de A.
Realizamos una recopilación de datos dados por el enunciado del problema:
· A ≡ 'Piezas producidas por la máquina A'.
· B ≡ 'Piezas producidas por la máquina B'.
· C ≡ 'Piezas producidas por la máquina C'.
· D ≡ 'Piezas defectuosas'.
· P(A) = 100/200 = 0.5.
· P(B) = 50/200 = 0.25.
· P(C) = 50/200 = 0.25.
· P(D|A) = 0.05.
· P(D|B) = 0.03.
· P(D|C) = 0.02.
Pasamos a resolver los distintos apartados del problema.
Apartado a)
En este apartado debemos obtener la probabilidad de que una pieza sea defectuosa, lo hacemos mediante la Ley de la Probabilidad Total:
La probabilidad de que una sea defectuosa es de 0.0375.
Apartado b)
En este problema, nos piden obtener la siguiente probabilidad (Ley de Bayes):

En estos momentos, disponemos de todos los datos necesarios para resolver este problema:
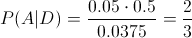
Por lo tanto, la probabilidad de que en caso de que la pieza sea defectuosa halla sido fabricada por la máquina A es de, aproximadamente, 0.666667.





2 comentarios:
A la hora de calcular la probabilidad de que una pieza sea defectuosa, en P(A), pones 0,05 y es 0,5 y el resultado de P(D)=17/400=0,0425. Gracias por el trabajo sólo comentar ese error. Saludos
Buenas:
Es cierto, ha habido un error a la hora de expresar el valor de P(A) cuando obtenemos la probabilidad P(D).
Aunque al final, el resultado estaba bien, ya que se utilizó el dato correcto. Aún así, ya está subsanado para no inducir a ningún tipo de error.
Lo que no me queda claro es de donde obtienes: P(D)=17/400=0,0425.
Un saludo y gracias por la corrección.
Publicar un comentario