Ej40. Una compañía dedicada al transporte público explota tres líneas periféricas de una gran ciudad, de manera que el 60% de los autobuses cubren el servicio de la primera línea, el 30% cubren el servicio de la segunda línea y el 10% cubren el servicio de la tercera línea.
Se sabe que la probabilidad de que, diariamente, un autobús se averíe es:
• Del 2% en la primera línea.
• Del 4% en la segunda línea.
• Del 1% en la tercera línea.
Determinar:
a) La probabilidad de que en un día un autobús sufra avería.
b) Sabiendo que un autobús ha sufrido una avería en un día determinado, ¿cuál es la probabilidad de que preste servicio en la primera línea?
Realizamos una recopilación de datos dados por el enunciado del problema:
· A ≡ 'Autobús que presta servicio en la primera línea'.
· B ≡ 'Autobús que presta servicio en la segunda línea'.
· C ≡ 'Autobús que presta servicio en la tercera línea'.
· D ≡ 'Autobús averiado'.
· P(A) = 0.6.
· P(B) = 0.3.
· P(C) = 0.1.
· P(D|A) = 0.02.
· P(D|B) = 0.04.
· P(D|C) = 0.01.
Pasamos a resolver los distintos apartados del problema.
Apartado a)
En este apartado debemos obtener la probabilidad de que en un día, un autobús sufra una avería, lo hacemos mediante la Ley de la Probabilidad Total:
La probabilidad de que en un día se estropee un autobús es de 0.025.
Apartado b)
En este problema, nos piden obtener la siguiente probabilidad (Ley de Bayes):
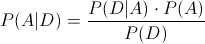
En estos momentos, disponemos de todos los datos necesarios para resolver este problema:
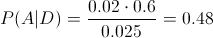
Por lo tanto, la probabilidad de que en caso de que se averíe un autobús, preste servicio en la primera línea, es de 0.48.





0 comentarios:
Publicar un comentario