Ej10. Un proceso tiene un índice de capacidad CCP = 2, pero la media está tres desviaciones típicas por encima del límite superior de especificación.
¿Cuál es la probabilidad de fabricar un producto dentro de los límites de las especificaciones?
Realizamos una recopilación de datos ofrecidos por el enunciado del problema:
· Cociente de Capacidad del Proceso: CCP = 2.
· La media está tres desviaciones típicas por encima de LSE: μ = LSE + 3σ.
Empleamos la expresión del CCP:
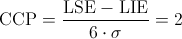
Despejamos:
LSE - LIE = 12σ
Definimos X a la característica de calidad, X~N(μ, σ), por lo tanto, lo que debemos obtener es:
P(LIE < .X < .LSE)
Al seguir X una distribución Normal, tipifico:
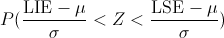
Sustituimos:
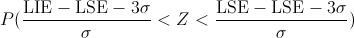
Por lo tanto:
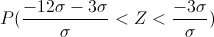
Simplifico:
P(-15 < .Z < .-3) = [1-(0.5+Φ(3))] - [1-(0.5+Φ(15))] = -Φ(3) + Φ(15)
Buscamos en la tabla de la Normal y obtenemos la solución a este problema:
P(LIE < .X < .LSE) = P(-15 < .Z < .-3) = -Φ(3) + Φ(15) = -0.4987 + 0.5 = 0.0013
La probabilidad de fabricar un producto dentro de los límites de las especificaciones es de 0.0013.





6 comentarios:
favor de indicarme cual es la tabla que utilizan para sacar esos valores, ya que en mi tabla de la distribucion normal solo tengo para sacar probabilidades de hasta Z=3.5
A partir de 3.5 se toma como valor 0,5
Hola. Yo no entiendo porque el valor 0.4987 es negativo y el de 0.5 positivo. Gracias
Buenas:
@mirko carvajal: En el menú de la izquierda podrás encontrar el apartado de Estadística, en él, está el apartado de Tablas Estadísticas donde hallarás la Tabla de la Distribución Normal y sus valores tipificados.
El valor es negativo ya que el signo es negativo, te desarrollo la expresión con más detalle:
· P(-15 < Z < -3) = - Φ(3) - (- Φ(15)) = - Φ(3) + Φ(15) = -0.4987 + 0.5 = 0.0013
Un saludo.
Gracias! y en probabilidades: cuando aplico P(..) o 1-P(--)? depende de que el proceso este fuera o bajo control? Gracias
Buenas:
Respecto a la probabilidad, depende de lo que te pidan, por ejemplo:
· P(A < X < B): Se obtiene la probabilidad de que la variable X esté entre los valores A y B.
· 1 - P(A < X < B): Se obtiene la probabilidad de que la variable aleatoria X no esté entre los valores A y B.
Un saludo.
Publicar un comentario